I když by se někdy mohlo zdát, že je přesný opak pravdou, většina vědců jsou celkem normální lidé s běžnými starostmi i radostmi. I oni mají rádi humor, takže není divu, že vymýšlejí různé zábavné kratochvíle. Jednou z nejoblíbenějších jsou sázky. To se obvykle dva nebo více vědců vsadí o nějaký vědecký výsledek, například, zda existuje či neexistuje Higgsův boson. Taková sázka musí mít samozřejmě přesně popsaná pravidla a určeny podmínky při jejichž splnění vyhrává jedna či druhá strana. Vědeckých sázek už známe v dnešní době stovky, některé mnohem slavnější než jiné. Dnes se ně některé z nejvýznamnějších sázek podíváme.

Protože toho máme ale opravdu hodně, rozhodl jsem se článek rozdělit na dvě části. Část první, jejíž začátek již vidíte níže, je věnována sázkám, které přímo, více či méně, souvisejí s kosmonautikou. U každé z nich naleznete aspoň malou souvislost s kosmickým výzkumem. Tato hlavní část článku zabírá něco málo přes polovinu celkové dálky textu. Část druhá je potom bonusová a je zaměřena na jiné zajímavé vědecké sázky, které už ovšem s kosmonautikou nemají žádnou souvislost (aspoň já jsem ji tam neobjevil). Takže jinými slovy, pokud vás zajímá opravdu jen a pouze kosmonautika, můžete klidně na konci první části se čtením přestat, nebudu se zlobit. Ale dle mého názoru by to byla trochu škoda, protože ve druhé části jsou některé velmi pozoruhodné a kuriózní případy vědeckých sázek.

Část I – kosmonautické a s kosmonautikou související sázky

Harmonie světů

Začneme několika sázkami, které se přímo, více či méně, týkají kosmonautiky. První z nich je stará už více než 400 let. Jak je to možné, říkáte si. V té době přece žádná kosmonautika neexistovala. A máte pravdu. Ale tehdy byl právě na vrcholu síly jistý pan Kepler, na jehož zákonech stojí kosmonautika dodnes.

Johannes Kepler, narozený v roce 1571, byl horlivým zastáncem heliocentrismu a Koperníkova učení a také velmi zdatný matematik. Právě na přelomu století, v roce 1600, odešel na pozvání císaře Rudolfa II. z Grazu do Prahy, aby spolupracoval s významným pozorovatelem, kterým nebyl nikdo menší než dánský astronom Tycho Brahe. Kepler začal analyzovat Braheho pozorování Marsu, aby přesně určil parametry jeho oběžné dráhy. S Brahem tehdy v Praze pobýval i jeho asistent Christen Sørensen Longomontanus s nímž se Kepler vsadil o to, jak dlouho mu bude na základě Braheho pozorování trvat vypočítat přesně parametry oběžné dráhy rudé planety.

Kepler byl vynikající matematik, a navíc nadšený z toho, že má přístup k tak cenným datům, a proto si velmi věřil. Vsadil tedy, že mu výpočet bude trvat jen týden. Longomontanus však znal Braheho data a domníval se, že doba nutná k úspěšnému dosažení cíle bude výrazně delší. A jak se ukázalo, nakonec měl pravdu. Určení dráhy Marsu se ukázalo být velkým oříškem. Bylo nutné sladit Braheho přesná, avšak geocentrická pozorování s Keplerovými vlastními představami. Keplerovi tak nakonec výpočet zabral více než pět let a Longomontanus tedy sázku jednoznačně vyhrál.

Není bohužel známo o co se oba muži vsadili. Avšak příliš mrzet nás to nemusí. Právě totiž na základě Braheho pozorování a snahy vypočítat přesné parametry dráhy Marsu vedly k důležitému objevu toho, že planety neobíhají Slunce po kružnicích, nýbrž po elipsách. Objevu o to cennějšímu, že Kepler odvrhl svůj ideál harmonického světa sfér, který však neodpovídal realitě. Tím se stal prvním moderním vědcem a o jeho přínosu bychom měli mluvit mnohem více. Alespoň jeho zákony pohybu planet se úspěšně aplikují i ve 21. století a jsou základní výbavou každého znalce kosmonautiky.

Největší z největších

Také druhá sázka se týká teoretického rámce kosmonautiky, jen tentokrát souvisí s osobou pravděpodobně největšího fyzika všech dob Isaaca Newtona a jeho dílem Principia. Věc má velmi zajímavou historii. V roce 1684 se totiž sešli v londýnské kavárně tři kamarádi. Ne, nejednalo se o postavy z díla spisovatele Ericha M. Remarqua, ale o tři přední osobnosti tehdejšího britského veřejného života.

Byli to Robert Hooke, Edmund Halley a Christopher Wren. První jmenovaný se proslavil především díky biologii. Jako první pozoroval buňky a také vymyslel termín anglický termín pro buňky „cell“. Nejmladší ze skupiny byl Halley, kterého naši čtenáři budou znát asi nejlépe. Právě po něm se totiž jmenuje proslulá Halleyova kometa. No a posledně jmenovaného možná znáte z hodin angličtiny na školách, protože to byl významný anglický architekt, který byl mimo jiné pověřen přestavbou Londýna po zničujícím požáru roku 1666.

Všechny tři muže však spojovala láska k fyzice a astronomii. Proto se při onom setkání v roce 1684 zamýšleli nad otázkou, jaký by byl matematický popis planety obíhající kolem Slunce v případě, kdy přitažlivá síla Slunce působící na planetu ubývá se čtvercem vzdálenosti. Jistě, výše zmíněný Kepler určil zákony pohybu planet, takže se všichni tři domnívali, že půjde o elipsu. Problém byl, že Kepler toto vypočítal na základě Braheho pozorování, neprovedl však matematický důkaz, a právě ten tato trojice požadovala. Sir Christopher Wren proto nabídl 40 šilinků (dnešních asi 2000 dolarů) tomu, kdo provede matematický důkaz toho, že planety obíhají kolem Slunce po elipsách.

V srpnu 1684 odjel Halley do Cambridge, aby se tam setkal s Isaacem Newtonem. Při debatě mu položil právě tuto otázku. Newton bez váhání odpověděl, že planety obíhají Slunce po elipsách. Halley chtěl vidět důkaz, který mu však Newton nebyl schopen v tu chvíli poskytnout, poslal ho až v listopadu 1684 v rámci devítistránkového pojednání „O pohybu těles na oběžné dráze“. Halley si brzy uvědomil, že Newton skutečně matematický důkaz poskytl, ale navíc přidal i další příspěvky týkající se dynamiky těles. Proto Newtona přesvědčil, aby co nejdříve připravil k vydání novou knihu Principia a zbytek už je, jak se říká, historie. Principia je dodnes považována za nejdůležitější kdy vydanou vědeckou knihu a Newtonovy zákony se dodnes v kosmonautice běžně používají.

Evoluce vs. plochá Země

Asi nikoho nepřekvapí, že i tvar Země byl předmětem jedné ze sázek. Byť dnes zakřivení Země můžeme běžně pozorovat při kosmických misích, v 19. století tomu tak nebylo. Proto vynálezce a spisovatel Samuel Rowbotham prováděl svérázné experimenty, které měly dokázat to, že je Země plochá. Nesetkal se ovšem s velkým zájmem. Ten přišel až o několik desetiletí později zásluhou jeho následovníka Johna Hampdena, který se vsadil s Alfredem Russellem Wallacem, geodetem, biologem a spoluobjevitelem teorie přírodního výběru (s Charlesem Darwinem), že plochost Země dokáže.

Klíčový experiment proběhl na 10 km dlouhém rovném úseku řeky Old Bedford v hrabství Cambridgeshire. Wallace jakožto geodet odhalil chyby předchozích měření, provedl správnou kalibraci a naměřil zakřivení Země přesně v souladu s teoretickými předpoklady a sázku vyhrál. To potvrdil i nezávislý rozhodčí, pan John Henry Walsh, redaktor sportovního časopisu The Field.

Tady by měl následovat konec příběhu, ale bohužel tomu tak není. Nepříliš překvapivě totiž Hampden svou prohru nepřijal. Vzápětí vydal brožuru, kde Wallace nařkl z podvodu a požadoval zpět své peníze. Následovaly pak dlouhé soudní přenice v jejichž průběhu si Hampden ještě přitížil, když Wallaceovi vyhrožoval zabitím. Ani Wallace však nevyvázl ze sporu zcela čistý. Mnozí kolegové jej kritizovali za neuvážené rozhodnutí se zapojit do sázky týkající se nejzákladnějších a nejprokázanějších vědeckých faktů.

Podobné experimenty byly ještě několikrát opakovány, avšak bez výraznější publicity. Dnes už máme k dispozici fotografie Země z družic na vysokých oběžných drahách, či dokonce fotografie z misí Apollo od Měsíce. Jakož i další data z družic dokazující, že Země plochá skutečně není. Víme však velmi dobře, že příznivce ploché Země žádné argumenty nepřesvědčí.

Byla whisky vypita oprávněně?

Objekt Cygnus A vyzařující v rádiové části spektra byl objeven v roce 1946 britskými astronomy Heyem, Parsonsem a Phillipsem. Zpočátku však nebyla jasná jeho povaha. Někteří, zvláště Martin Ryle se domnívali, že se jedná o nový typ hvězdy viditelný v rádiovém spektru, opticky však neviditelný. Jiní, zejména Thomas Gold a Fred Hoyle se naopak domnívali, že jde o extragalaktický zdroj, zřejmě tedy nějaký typ galaxie. Spor nakonec vyřešil v roce 1951 americký astronom německého původu Walter Baade, který nade vší pochybnost dokázal, že se Cygnus A nachází mimo Mléčnou dráhu.

Baade se také domníval, že Cygnus A jsou ve skutečnosti dvě srážející se galaxie. To se Baademu navíc velmi hodilo, jelikož začátkem téhož roku publikovali s Lymanem Spitzerem článek o srážejících se galaxiích. Další astronom Rudolph Minkowski si této nápadné shody všiml a utrousil na toto téma několik ironických poznámek. To Baadeho naštvalo a vyzval Minkowského na sázku o 1000 dolarů, že Cygnus A je srážka galaxií. Minkowski sázku přijal, nicméně výhra byla snížena na lahev whisky. Oba muži se shodli i na důkazu. Kdyby byly pozorovány emisní spektrální čáry s vysokou excitací. Ty jsou totiž produkovány atomy a ionty v plynu s nízkou hustotou, avšak vysokou teplotou před deset tisíc Kelvinů. Naopak u hvězd převažují absorpční čáry z relativně chladných atmosfér.

Minkowski o několik týdnů později pořídil spektrum objektu Cygnus A pomocí dalekohledu na observatoři Mount Palomar a byť nebyly výsledky přesně podle Baadeho očekávání, svou porážku uznal. Přinesl tedy Baademu výhru. Baade tvrdil, že lahev je podle něj litr, Minkowski ovšem přinesl placatku. Věc měla ovšem ještě zajímavou dohru. O dva dny později, totiž Minkowski Baadeho znovu navštívil, aby ho seznámil s novým zajímavým výsledkem, všiml si placatky a v roztržitosti ji vypil. Baade tedy z výhry neměl nic. Paradoxní je, že o 12 let později byly učiněny nové důležité objevy, které dávají za pravdu Minkowského hypotéze, že Cygnus A srážka galaxií není. Minkowski tak přece jen vypil placatku po právu.

Dnes je na nesrážkovém původu objektu Cygnus A (také 3C 405, jakožto objekt třetího Cambridgeského katalogu rádiových zdrojů) mezi astronomickou a astrofyzikální komunitou obecná shoda. Galaxie je častým cílem mnoha předních vědeckých observatoří, ať už jsou to radioteleskopy typu soustavy VLA v Novém Mexiku v USA, nebo kosmické teleskopy pracující v rentgenovém spektru. Cygnus A byla například jedním z prvních cílů americké observatoře Chandra, která nedávno slavila 25 let v kosmickém prostoru.

Válka o černé díry

Dalším sporem o podstatu kosmického objektu byla pře o rentgenový zdroj Cygnus X-1. Jedná se o velmi slavný objekt, který se dostal i do populární kultury. Objeven byl v roce 1964 při suborbitálním letu sondážní rakety startující ze základny White Sands v Novém Mexiku v USA. Další pozorování, včetně měření kosmické rentgenové observatoře Uhuru v roce 1970, nakonec ukázala, že oblast, z níž se rentgenové záření uvolňuje musí být velmi malá. Proto převážila myšlenka, že se ve skutečnosti jedná o tehdy dosud hypotetický objekt, černou díru. Tedy objekt tak kompaktní, že z něj nemůže uniknout nic, ani světlo.

A jak to, že tuto černou díru vidíme, když černá díra nemůže žádné světlo vyzářit? Inu, my nevidíme černou díru samotnou. V tomto případě máme ovšem štěstí, protože předpokládaná černá díra je v soustavě s jinou velmi hmotnou hvězdou hlavní posloupnosti. Černá díra svou silnou gravitací přetahuje z této hvězdy materiál, který padá směrem k ní a rozprostírá se kolem černé díry v tzv, akrečním disku, tedy disku materiálu obíhajícím tuto černou díru. Fyzikální procesy v akrečním disku pak způsobují vzájemné interakce částic hmoty v disku a následně jeho zahřívání, což vede k uvolňování značného množství rentgenového záření.

V roce 1973 už byla většina fyzikální komunity přesvědčena, že systém Cygnus X-1 obsahuje černou díru. Přesto se na konci roku 1974 legendární fyzik Stephen Hawking vsadil se svým jen o něco méně slavným kolegou Kipem Thornem, že Cygnus X-1 černou díru neobsahuje. V roce 1990 poté, kdy došlo ke zveřejnění dalších a přesnějších pozorování, Hawking uznal svou porážku a zajistil Thorneovi jeho výhru, roční předplatné pánského časopisu Penthouse, k veliké nelibosti Thorneovy manželky.

Zarazili jste se u předchozího odstavce? Že ne? Ale to byste měli! Stephen Hawking je totiž velmi proslulý zejména díky své práci v oblasti černých děr. Jeho nejslavnější práce z této oblasti, která se věnuje termodynamice černých děr a postuluje tzv. Hawkingovo záření dokonce roku uzavření sázky (1974) předchází. Takže jak je možné, že Hawking klidně uzavřel s Thornem sázku na to, že Cygnus X-1 není černá díra, když se zkoumání těchto objektů již v té době intenzivně věnoval?

Hawking v tomto případě nepostupoval dle svého přesvědčení, ale jednal takticky. Prohlásil, že v případě, kdy by se náhodou ukázalo, že černé díry neexistují a on vyhodil mnoho let života zkoumáním něčeho neexistujícího, chtěl z toho aspoň něco mít. Tedy výhru v této sázce s Thornem. Myslím však, že ho konečný výsledek, kdy se ukázalo, že Cygnus X-1 černou díru obsahuje, potěšil mnohem více.

Hawking – mistr porážek

Mimochodem, než se vydáme k jiným vědcům, chtěl bych se aspoň stručně vyjádřit k dalším Hawkingovým sázkařským úspěchům, respektive spíše neúspěchům. Hawking se totiž s kolegy vědci sázel velmi rád, jeho úspěšnost však byla mizerná. Všechny nejvýznamnější sázky prohrál. O jaké sázky šlo?

Z roku 1991 pochází sázka, kterou Hawking uzavřel s kolegy relativisty Johnem Preskillem a Kipem Thornem (opět). Týkala se tzv. nahých singularit, tedy singularit, které by existovaly volně v prostoročasu bez horizontu událostí černé díry. Hawking se domníval, že fyzika existenci nahých singularit zakazuje, naopak Preskill a Thorne se domnívali, že existovat mohou. V roce 1997 Hawking přiznal prohru, když na základě výsledků matematických fyziků připustil, že existence nahých singularit je technicky možná za určitých velmi specifických podmínek.

Další sázka, uzavřená jen den poté, kdy Hawking uznal porážku v sázce předchozí, se opět týkala černých děr a složení sázejících bylo totožné, tedy Preskill, Hawking a Thorne. V tomto případě šlo o tzv. informační paradox. Podle obecné relativity by totiž veškerá informace, která jednou spadla do černé díry, měla být navždy ztracená. Naopak podle kvantové mechaniky by tato informace měla být zachována a mělo by ji být možné, aspoň v principu, z černé díry získat. Tentokrát Preskill vsadil na zachovávání informace, zatímco Thorne a Hawking vsadili na to, že se informace ztrácí. A v roce 2004 Hawking přiznal porážku i v této sázce. Proč?

Jednak sám Hawking tvrdil, že paradox vyřešil ve prospěch Preskilla. Jednak Argentinský fyzik Juan Maldacena dokázal, že se informace zachovávají, a to i po pádu do černé díry. Věc má jen jeden malý drobný problém. Maldacena to totiž prokázal pro tzv. anti-de Sitterovský prostor, což je velmi zjednodušeně prostor s konstantní zápornou křivostí. Jenže takový náš vesmír není. Z toho důvodu Thorne porážku v této sázce neuznal a navzdory Maldacenově důkazu a Hawkingovu přiznání porážky dosud není situace zcela uspokojivě vyjasněna. I tak Hawking poskytl Preskillovi jeho výhru, tedy encyklopedii baseballu. Nicméně i pokud lze informaci z černé díry získat, nelze ji rekonstruovat do původní podoby. Proto Hawking žertoval, že měl Preskillovi raději darovat popel.

Poslední sázkou, která stojí za zmínku je sázka, kterou Hawking uzavřel s americkým fyzikem Gordonem Kanem. Týkala se proslulé částice známé jako Higgsův boson. Hawking tvrdil, že neexistuje, Kane, že ano. Higgsův mechanismus byl původně objeven několika skupinami fyziků v roce 1964 a jeho existence se brala za téměř jistou, byly však představitelné i scénáře, kde by sice mechanismus platil, avšak negeneroval by Higgsův boson. Jak však víme, v roce 2012 byl na urychlovači LHC v CERNu Higgsův boson objeven, a tak Hawking vyplatil Kaneovi jeho výhru 100 amerických dolarů.

Jak získat sto galonů benzínu

Ani kosmologii se sázky nevyhnuly. V 80. letech se teoretický astrofyzik Frank Shu vsadil s pozorovatelem Georgem Djorgovskim, že teoretikové dokáží do 1. ledna 2001 určit základní kosmologické parametry vesmíru, například jeho věk či celkovou hustotu, určit natolik přesně, že pozorovatelé už budou mít práci „jen“ s ověřením jejich teoretických předpovědí. O pár let později se zdálo, že se teoretické kosmologii daří velmi dobře, proto paradoxně právě pozorovatel George Djorgovski uzavřel podobnou sázku s teoretikem Davidem Spergelem. Kuriózní na tom bylo, že Djorgovski věřil teoretikům, zatímco naopak Spergel vsadil proti teoretikům, ačkoliv byl sám teoretik.

Situace s teoretickými předpověďmi nakonec zdaleka nebyla tak růžová, z toho důvodu situace byla naopak taková, že přesnější kosmologické parametry určila až pozorování kosmických observatoří, jako byly mise COBE či WMAP. Teoretici v tomto případě prohráli na celé čáře. Spergel tak vyhrál, Shu prohrál a Djorgovski jednu sázku vyhrál a druhou prohrál. Nejvíce kuriózní na první sázce Shu vs. Djorgovski je fakt, že jako výhra bylo stanoveno 100 galonů benzínu. Sázka totiž byla uzavřena v době vrcholící ropné krize, kdy byl benzín poměrně drahý a vzácný.

Je změna klimatu reálná?

Dalším ochotným sázejícím je britský klimatolog James Annan. Ten se během let několikrát snažil vsadit s popírači globálních změn klimatu, většinou však k dohodě nedošlo. Až v roce 2005 se vsadil s dvojicí ruských slunečních fyziků Galinou Mašnych a Vladimirem Baškircevem o 10 000 amerických dolarů o průměrnou globální teplotu. Anna tvrdil, že průměrná globální teplota v letech 2012–2017 bude vyšší než průměrná globální teplota v letech 1998–2003, zatímco Rusové tvrdili opak. Data dala za pravdu Annanovi, své chýry se ovšem nedočkal. Ruští vědci prostě odmítli zaplatit.

Annan vyhrál i celou řadu dalších sázek, ostatně není divu, data o globální změně klimatu hovoří jasnou řečí. Data, pro jejichž získání jsou mimochodem zcela zásadní družice určené k pozorování Země. Takže ano, i v tomto je kosmonautika zastoupena, dokonce velmi významně. I přes výše uvedené však Annan jednu sázku i prohrál. A to, když se v roce 2011 vsadil s astrofyzikem Davidem Whitehousem. Annan totiž tvrdil, že průměrná roční teplota měřená britskou službou Met Office v roce 2011 překoná rekord a rok 2011 tak bude nejteplejším v historii měření. Přestože výsledek nebyl nakonec zcela jasný, Annan porážku uznal a výhru zaplatil. Nutno dodat, že v řadě jiných let by Annan vyhrál, Whitehouse měl v tomto případě do značné míry velké štěstí.

Kde najdeme mimozemský život?

Velmi zajímavou sázku uzavřeli v roce 2002 astrofyzik Freeman Dyson a podnikatel Peter Spark. A to prostřednictvím webové stránky longbets.org. Pro ty, kteří se rádi sázejí jde o velmi zajímavý web, kde si mohou prohlížet již uzavřené a vyhodnocené sázky, sami vytvořit predikce a vyzvat někoho z místní komunity k uzavření sázky anebo sami přijmout výzvu někoho, kdo učinil jednu ze zajímavých predikcí. Podmínky jsou zde v zásadě velmi jednoduché:

„1. Každá sázka se týká něčeho významného. Nejčastěji tedy něčeho z oblasti vědy, umění, politiky, či společnosti. 2. Minimální dobu, na niž lze sázku uzavřít jsou dva roky, maximální doba omezena není. 3. Sázka není dohad. Každý sázející musí předložit své argumenty proč sází na to či ono. 4. Minimální výše sázky je 200 dolarů. 5. Výhra, ať už vyzyvatele, nebo autora předpovědi, jde na dobročinné účely, nadaci má právo si určit autor, respektive vyzyvatel.“

Ale zpět k sázce Dysona a Sparka. Ta se týká toho, jestli bude první objev mimozemského života učiněn na (exo)planetě nebo jejím měsíci. Freeman Dyson, známý nejen díky svým vynikajícím fyzikálním výsledkům, zejména v oblasti kvantové elektrodynamiky, ale též jako futurista navrhující Dysonovy sféry nebo nukleární pulsní pohon, argumentoval, že by se život mohl přizpůsobit životu ve vakuu. Naopak Peter Spark tvrdil, že nalezení života na planetě nebo měsíci je pravděpodobnější.

Sázka byla uzavřena na dobu neurčitou, tedy dokud nedojde k rozhodnutí v podobě prvního objevu mimozemského života. Jak víme, Freeman Dyson zemřel v roce 2020 ve věku 96 let, takže do sázky byly později přidány dva dodatky. První říká, že pro účely sázky se život definuje jako sebereplikující se buněčný organismus. Druhý říká, že v případě nějakého objevu bude rozhodnutí o tom, zda lze to, co bylo objeveno, klasifikováno jako život, ponecháno na Georgi Dysonovi (syn Freemana) nebo jeho potomcích. Jak tedy vidíte, sázka pokračuje i přes úmrtí jednoho ze sázejících.

Kdy se dočkáme mezihvězdného letu?

Na stránce longbets.org se můžeme setkat i s několika dalšími sázkami úzce souvisejícími s kosmonautikou. Jednou z nich je sázka, kterou spolu uzavřeli fyzik Tibor Pacher a spisovatel Paul Gilster. Byla uzavřena v roce 2008 a její znění je: „První skutečná mezihvězdná mise zaměřená na hvězdu nejblíže Slunci, nebo i dále, bude vypuštěna před 6. prosincem 2025 nebo v ten den a bude mít širokou podporu veřejnosti.“

Sobota 6. 12. 2025 bude brzy a jak víme, žádná taková mise se nechystá, takže ačkoliv to ještě není zcela akurátní, de facto můžeme za vítěze již nyní prohlásil spisovatele Gilstera a fyzika Pachera označit za poraženého. Zajímavé je, že Gilster se věnuje psaní sci-fi, takže byste možná čekali, že bude optimistický a od fyzika naopak, že bude skeptický, ale není radno věřit předsudkům. Každopádně se oba pánové shodli, že k mezihvězdnému letu jednou dojde, jen Gilster tvrdil, že to bude zřejmě výrazně později oproti termínu určenému sázkou, pokud tedy nedojde k nějakému zásadnímu technologickému průlomu, což jak víme nedošlo.

Zajímavé jsou i stanovené podmínky, kde se uvádí: „1. Mise může být pilotovaná i nepilotovaná. Musí však jít o misi cíleně navrženou pro průzkum jiné hvězdy, tedy ne mise ke zkoumání vnější Sluneční soustavy, která bude pokračovat dále. 2. Povoleným místem startu je jakékoliv místo ve Sluneční soustavě po oběžnou dráhu Neptunu, a to jak povrchy těles, tak kosmické stanice či jiné místo v prostoru. 3. Mise musí být schopna dodat alespoň jedno vědecké měření (jakékoliv). 4. Doba mise musí být kratší než 2000 let. 5. Podpora široké veřejnosti se definuje například jako osvětová akce, v jejímž rámci bylo nasbíráno 1 000 000 podpisů na podporu mise. Bod číslo 5. však není rozhodující pro vyhodnocení sázky.“

Pozoruhodné je, že bylo stanoveno, že v případě výhry vyzyvatele Gilstera půjde výhra v hodnotě 1 000 amerických dolarů na podporu nadace Tau Zero, která se právě snaží pracovat na první mezihvězdné misi lidstva. Určení ceny je tedy vskutku příznačné. A myslím, že se shodneme, že vzhledem k podmínkám sázky se nadace této částky velmi brzy dočká.

Bude muset kolega Dušan pojíst zubní kartáček?

Z této sázky by měl velkou radost náš šéf Dušan Majer. Uzavřeli ji v roce 2020 biolog Andrew Burchill a kosmický inženýr Thomas Davis. Opět citujme její znění: „Do roku 2035 bude žít na Marsu nejméně 10 osob po dobu delší než 2 měsíce.“ Biolog Burchill argumentuje, že lidstvo brzy přestane v průzkumu vesmíru stagnovat, a tedy se dočkáme výrazných technologických inovací. Proto věří, že lidé do uvedeného roku na Marsu žít budou. Naopak inženýr Davis je skeptický, tvrdí, že 15 let je příliš málo a argumentuje, že než se budou moci lidé na Marsu usídlit, bude to vyžadovat příliš mnoho pokusů a omylů na to, aby bylo možné termín stihnout.

Pro účely sázky se stanovuje, že do 31. prosince 2035 musí žít na povrchu Marsu deset lidí po dobu dvou pozemských měsíců nebo více, přičemž musí jít o stejné lidi. Pokud by šlo například o dvě mise po jednom měsíci, nepočítá se to do stanoveného limitu. Pozemský měsíc se definuje jako 30 dní a doba přeletu ze Země na Mars a případná doba strávená na oběžné dráze Marsu se do limitu nezapočítává. Ať už vyhraje kdokoliv, výhra půjde na Australskou nadaci věnující se výzkumu autismu.

Stejného tématu se týká i další sázka, respektive předpověď, protože tuto výzvu dosud nikdo nepřijal. Matematik Benjamin Thompson tvrdí, že do konce roku 2035 bude žít na Zemi alespoň jeden člověk, který chodil po Marsu. Argumentuje přitom nedávnými úspěchy SpaceX a jejím partnerstvím s NASA, jakož i plánovaným přistáním na Měsíci s misí Artemis III. Výzva byla podána v roce 2020, takže bude platit ještě 10 let. Pokud ji snad zde někdo chce přijmout může, jen nezapomeňte, co jsem psal výše. Je třeba uhradit 200 dolarů, sepsat svoje argumenty a vybrat nadaci, které připadne případná výhra.

Najde JWST mimozemský život?

Dalekohled Jamese Webba je bezesporu výkvětem moderní techniky. Dokáže ale najít mimozemský život? Právě to tvrdí vědec Joseph McCord, který navíc dodává, že tento život bude fotosyntetizující a JWST najde jeho důkazy na některé z exoplanet. McCord argumentuje tím, že dnes již známe tisíce exoplanet a mnohé z nich se nachází v obyvatelné zóně své hvězdy. Navíc se naše schopnost analyzovat spektra exoplanet významně zlepšila. Domnívá se proto, že důkaz mimozemského života JWST poskytne do roku 2034.

Jde o sázku, o níž vážně uvažuji, že bych se zde stal vyzyvatelem a argumentoval proti tvrzení pana McCorda. Protože mám za sebou několik kurzů astrobiologie, vím, jak obtížné je najít biosignatury, natož je správně interpretovat. Je otázka, co by vůbec mohlo být považováno za definitivní a nezpochybnitelný důkaz života na exoplanetě. Pan McCord argumentuje velkým množstvím kyslíku, jindy se objevují tvrzení o dimethylsulfidu. U všech těchto sloučenin je však představitelný i abiotický vznik, navíc by pozorování muselo být velmi přesvědčivé, jinak se dá vždy argumentovat chybou měření. A třeba ani pozorování štěpné jaderné reakce na exoplanetě není důkazem života, neboť jak víme z gabonské lokality Oklo, i jaderné reaktory mohou vznikat přirozeně.

Skončí pilotovaná kosmonautika v režii NASA?

Jakob Conner se domnívá, že ano, a to dokonce už v letošním roce. Před sedmi roky, v roce 2018 podal výzvu, kde tvrdí, že v roce 2025 již nebude americká NASA mít vlastní pilotovaný program. Argumentuje, že rychlý rozvoj společností jako SpaceX, Virgin a další NASA z oblasti pilotovaných letů do vesmíru zcela vytlačí a pilotované programy NASA tak zůstanou pouhou minulostí.

Výzvu nikdo nepřijal, takže zůstane bez vítěze. Bohužel v tomto případě není výzva příliš konkrétní, takže se neuvádí, co přesně znamená konec NASA v pilotovaných letech. Tedy například nevíme, zda lety Crew Dragonů, které si NASA u SpaceX objednává se počítají jako mise NASA či nikoliv. Objektivní skutečnosti teď nechme stranou, důležité je, jak by byly definovány v případě přijetí sázky. Ať tak či onak, program Artemis zatím stále probíhá a pokud nebude do konce roku úplně zrušen, předpokládám, že by sázku vyhrál případný vyzyvatel, neboť Artemis je v režii NASA.

Bude muset SpaceX čelit kosmické srážce?

Chris Rodriguez, který sám sebe označuje jako vesmírného nerda vypsal v roce 2021 výzvu, která tvrdí, že se do roku 2040 satelit vyrobený společností SpaceX srazí v kosmickém prostoru s jiným objektem. Předkládá, celkem pochopitelně, argument týkající se neustálého prudkého zvyšování počtu družic na oběžné dráze v posledních letech. A byť existují i plány jiných megakonstelací, prozatím jasně vede právě SpaceX se svou sítí Starlink. O tom, zda u Starlinků převažují pozitiva či negativa jistě můžeme dlouze diskutovat, nám teď však jde o onu výzvu, jejíž splnění se jeví poměrně pravděpodobné. Satelitů SpaceX je v kosmu poměrně dost, a navíc je tato výzva platná do roku 2040, takže i nyní zbývá 15 let. Možná proto ji dosud nikdo nepřijal.

Byť ano, i zde samozřejmě záleží, jak přesně by se stanovily podmínky ohledně toho, co to je satelit Space X a co to je jiný objekt v kosmickém prostoru. Rodriguez zde předkládá aspoň základní tvrzení, že satelit v jeho pojetí může být aktivní i již nefunkční, ale nejde o horní stupně raket či trosky raket. Horní stupně či trosky nosných raket však dle něj mohou být považovány za další objekty v kosmickém prostoru, tedy pokud by se s nimi satelit Space X srazil, vyhrál by Rodriguez. Byť opět, záleží, co považujeme za „objekt“. Zda například milimetrová součástka nebo kousek laku by se považoval za další objekt v kosmickém prostoru tak, aby byly splněny podmínky sázky. Vzhledem k tomu, že ale zatím výzvu nikdo nepřijal, není třeba se tím příliš trápit.

Část II – nekosmonautické sázky

Neobyčejný génius

Hrdinou této podkapitoly je legenda americké fyziky Richard Feynman, známý i díky své roli ve vyšetřování havárie raketoplánu Challenger. Jeho vášeň v sázkách však Challengeru o mnoho desetiletí předchází. První zajímavou sázku, respektive sázky musíme hledat v 50. letech. Tehdy se hodně řešila tzv. P symetrie, velmi zjednodušeně řečeno symetrie mezi pravou a levou stranou. Tedy jinými slovy, pokud platí P symetrie, pak při zrcadlovém převrácení systému nedokážeme žádným experimentem poznat rozdíl oproti původnímu stavu. Feynman se vsadil, že se tato symetrie zachovává, ale prohrál. Narušení P symetrie předpověděli fyzikové C. N. Yang a T. D. Lee a experimentálně jej prokázala fyzička C. S. Wu. Příroda tedy rozlišuje mezi pravou a levou stranou.

V 50. letech přišel na Caltech, kde tehdy Feynman působil také další proslulý génius Murray Gell-Mann. Tito dva muži byli dobří přátelé, současně však i dva kohouti na jednom smetišti. Intelektuální spory tedy mezi nimi byly časté. Jednou například Feynman přišel do Gell-Mannovy kanceláře a stěžoval si na jakousi podivnou paní, která mu telefonovala a představovala mu svou pochybnou teorii magnetismu a on se jí vůbec nemohl zbavit. Gell-Mann Feynmanovi prozradil, že mu tato paní také volala, ale rozhovor s ní dokázal ukončit během půl minuty. Feynman byl ohromen a zajímal se, jak to Gell-Mann dokázal. Gell-Mann mu prostě odvětil, že paní řekl, že má zavolat Feynmanovi, neboť on je skutečným odborníkem na toto téma.

Skeptik a popularizátor Al Seckel jednou pozval Feynmana a Gell-Manna na stejnou párty, což se brzy ukázalo jako velká chyba. Celý večer totiž strávili ti dva vzájemným rozhovorem, kdy vždy jeden přednesl nějakou zajímavost, na což druhý reagoval tím, že to přece už dávno věděl a nemusel to tudíž říkat. Později někdo u stolu něco pronesl a Gell-Mann briskně zareagoval, že jde o pleonasmus. Na nechápavé pohledy odvětil, že to je věta s několikanásobnou redundancí. Feynman a Seckel to rychle ověřili ve slovníku a zjistili, že měl pravdu. Feynman se naštval a nechápal, jak může mít Gell-Mann vždycky pravdu.

Téhož večera ještě později došla řeč na čarodějnictví a inkviziční procesy s čarodějnicemi. Gell-Mann se obecenstva otázal, zda znají knihu Malleus Maleficarum, kterou napsal anglický král Jakub I. v roce 1623. Seckel zavětřil a okamžitě odpověděl, že se Gell-Mann mýlí, neboť tuto knihu napsali Kramer a Sprenger v roce 1486, zatímco král Jakub I. napsal publikaci Démonologie z roku 1597. Feynman vytušil možné vítězství, ale ještě bylo třeba tuto skutečnost dokázat. Seckel vzápětí vyhledal tuto informaci v encyklopedii a potvrdil tak pravdivost svých slov. Feynman se začal smát, až spadl pod stůl a opakoval Gell-Mannovi, že mu tohle nikdy nezapomene.

Poslední zajímavá Feynmanova sázka souvisí s Nobelovou cenou, kterou obdržel v roce 1965 za kvantovou elektrodynamiku. Známý fyzik rakouského původu Victor Weisskopf se domníval, že Feynman od té chvíle nebude mít čas na vědu a bude se věnovat jen administrativě. Feynman nesouhlasil, a tak uzavřeli sázku o deset dolarů. Ve smlouvě je uvedeno, že pokud Feynman v příštích deseti letech bude zastávat jakoukoli odpovědnou funkci, vyhrává Weisskpf, naopak pokud ji zastávat nebude, vítězí Feynman. Odpovědná funkce se pro účely sázky chápe jako funkce, která svou povahou nutí držitele vydávat jiným osobám pokyny k provedení určitých úkonů a to přesto, že držitel funkce vůbec nerozumí tomu, co uvedeným osobám nařizuje. Netřeba asi zdůrazňovat, že Feynman vyhrál.

Tak na život bez odpovědných funkcí.

Porazí počítač lidského šachistu?

Skotský mezinárodní šachový mistr David Levy hrál jednoho letního večera roku 1968 přátelskou hru v šachu se svým přátelem, počítačovým vědcem a profesorem ze Stanfordovy univerzity Johnem McCarthym. Samozřejmě jej suverénně porazil. Po zápase McCarthy prohlásil, že do roku 1978 bude existoval program, který porazí i tak skvělého šachistu, jako je právě Levy.

A sázka byla na světě. Levy nejprve vsadil 500 liber, proti McCarthymu, že v obdoví následujících deseti let, tedy do roku 1978, neprohraje jediný šachový zápas proti počítači. Hned vzápětí se k dohodě přidali další tři odborníci na umělou inteligenci a počítače a sázka byla zvýšena na 1250 liber. Levy skutečně ve smluveném období proti počítači neprohrál a to dokonce ani, když proti němu jeho soupeři v roce 1978 nasadili Chess 4.6, tehdy nejsilnější šachový počítač světa, takže si svou výhru zcela zasloužil.

Sluší se podotknout, že první šachový program, který porazil mistra světa v šachu byl Deep Blue v legendárním zápase s tehdejším mistrem světa Garri Kasparovem, který se konal v roce 1997. Tehdy to bylo vydáváno za úžasný pokrok umělé inteligence. No, dnes víme, že si můžeme koupit za pár dolarů šachový program, který porazí každého šachistu na světě s výjimkou několika nejlepších velmistrů, ale přesto si nikdo nemyslí, že by tento program byl jakkoli inteligentní.

Kolik genů obsahuje lidský genom?

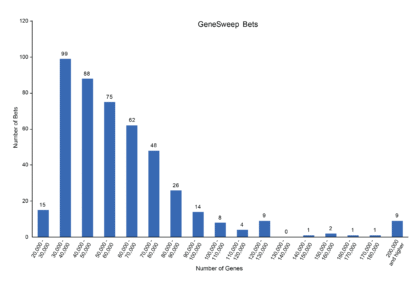
Ne každá vědecká sázka musí mít nutně podobu toho, že se vsadí dva nebo tři stárnoucí bílí heterosexuální muži. Občas mají sázky také podobu výzvy nebo tipovačky, do níž se přihlásí stovky vědců. Nejznámějším podobným příkladem je výzva GeneSweep, v jejímž rámci měli vědci možnost tipovat či odhadovat, kolik genů je celkově obsaženo v lidském genomu. Výzva byla zahájena v roce 2000 na konferenci v laboratoři Cold Spring Harbor v New Yorku v USA a zúčastnilo se jí 460 vědců. Výhra činila 1200 dolarů. Ovšem nikoli pro toho, kdo počet genů určil přesně, nic takového se neočekávalo, ale pro toho, kdo byl zjištěnému počtu nejblíže. Průměrný počet genů, které sázející tipovali byl 62 598 a kupříkladu Nobelista James Watson sázel na počet 73 210.

Vítěz byl oznámen v květnu 2003 a stal se jím Lee Rowen z Institutu pro systémovou biologii v americkém Seattlu. Rowen odhadoval, že lidský genom se skládá z 25 947 genů, což bylo nejblíže číslu 24 847, který uváděl evropský projekt genomové databáze Ensembl. Povšimněte si tak, že skutečný i vítězný počet je výrazně nižší než průměrný odhadovaný počet zmíněný výše. Současně je Rowenův tip také nejnižší. Vítěz připsal zásluhu za tento fakt francouzskému biologovi Jeanu Weissenbachovi ze sekvenčního centra Genoscope ve francouzském Évry, který jej přesvědčil, že počet genů bude relativně nízký. Rowen se o výhru podělil s kolegy Olivierem Jaillonem z Francie a Paulem Dearym z Anglie, což byly jediní dva další, kteří odhadovali počet genů nižší než 30 000.

Co všechno se může objevit ve vědeckém článku?

John Ellis je britsko-švýcarský teoretický fyzik, který se zabývá astrofyzikou, částicovou fyzikou, kosmologií či kvantovou fyzikou. V polovině 70. let se intenzivně věnoval standardnímu modelu, konkrétně se zabýval s Mary Gaillard a Dimitrim Nanopoulosem narušením CP symetrie (C je symetrie mezi hmotou a antihmotou, P symetrie mezi pravou a levou stranou) ve standardním modelu a také kvarkům, Gaillard, Nanopoulos, Ellis a Serge Rudaz společně předpověděli vlastnosti b kvarku ještě předtím, než byl experimentálně pozorován. Když k jeho potvrzení o několik týdnů později došlo, začala skupina pracovat na jeho podrobnějším popisu.

Tehdy byla v CERNu na stáži fyzička Melissa Franklin, dnes pracovnice Harvardovy univerzity. John Ellis, Melissa Franklin a Serge Rudaz šli jednou večer do hospody a začali hrát šipky. Franklin a Ellis se vsadili, že pokud Ellis prohraje, musí do své další vědecké práce napsat slovo tučňák. Melissa Franklin ovšem šipky opustila ještě před rozhodnutím, nahradil si Serge Rudaz a ten Ellise porazil. Ellis se tedy mohl vymlouvat, že podmínky byly porušeny, ale cítil se sázkou zavázán, a tak se rozhodl ji splnit. Nějakou dobu marně přemýšlel, jak slovo tučňák zakomponovat, asi uznáte sami, že tučňáci jsou od fyziky dosti vzdáleni. Pak ho ovšem napadlo, že typ Feynmanových diagramů, který popisu interakce kvarků vypadá docela jako tučňák. A tak se zrodilo něco, čemu dnes říkáme tučňákové diagramy.

Proč jsou některé částice přátelské a jiné nepřátelské?

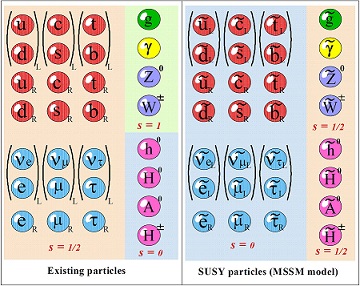
Koncept supersymetrie byl vymyšlen na počátku 70. let několika skupinami teoretických fyziků. Základní myšlenka je poměrně jednoduchá. Jak možná víte, v částicové fyzice rozlišujeme dva základní typy částic – bosony a fermiony. Bosony, jejichž zástupcem je třeba Higgsova částice nebo foton, mají celočíselný spin a Pauliho vylučovací princip pro ně neplatí. To znamená, že klidně můžeme mít velké množství bosonů v jediném kvantovém stavu. Naproti tomu fermiony, jejichž zástupci jsou elektrony nebo kvarky, mají poločíselný spin a Pauliho vylučovací princip pro ně platí. Tedy nelze mít žádné dva fermiony se stejnými kvantovými čísly v témže kvantovém stavu. Díky tomu mohou existovat složité struktury. Kdyby byly všechny částice bosony, nic z toho, co vidíme kolem sebe, by nemohlo existovat.

Někoho ale napadlo, že je přece velmi nefér, že bosony jsou přátelské částice a mohou být pohromadě a fermiony nikoliv. A taky vznikl koncept supersymetrie, který předpokládá existenci další sady částic, tzv. superpartnerů. Každý běžný boson by měl superpartnera fermion (např. elektron a selektron) a každý běžný fermion by měl superpartnera boson (např. foton a fotino). Tím by se tato nespravedlnost vyrovnala. Supersymetrie by řešila některé dosti důležité fyzikální problémy, jeden ze superpartnerů by třeba mohl vysvětlovat i temnou hmotu. Jenže bohužel, dosud žádný experiment superpartnery nepozoroval. Řada vědců si tak začíná myslet, že supersymetrie je sice zajímavý koncept, avšak v našem vesmíru nerealizovaný.

Jsou však i fyzikové, kteří supersymetrii stále věří a v důsledku toho vzniká mnoho sázek na to, zda supersymetrie platí či nikoliv. V létě roku 2000 se například 40 fyziků vsadilo, že urychlovač LHC v CERNu najde některého ze superpartnerů. Sázka původně platila do roku 2011, později byla kvůli zpoždění urychlovače prodloužena do roku 2016. Když ani tehdy žádné známky supersymetrie nebyly nalezeny, poražení dodali protistraně výhru, koňak v hodnotě asi 100 amerických dolarů. Na supersymetrii vsadili i někteří Nobelisté za fyziku. V roce 2008 to byl Frank Wilczek, který uzavřel sázku s Anthony Garrettem Lisim a v roce 2016 David Gross, jenž se vsadil proti Zvi Bernovi. Gross i Wilczek sázky prohráli, přesto se stále domnívají, že se existenci supersymetrie brzy podaří dokázat.

Objasníme brzy, co to je vědomí?

Jednu z nejslavnějších sázek posledních desetiletí spolu v roce 1998 uzavřeli neurovědec Christof Koch a filosof David Chalmers v roce 1998 a týkala se podstaty lidského vědomí. Jejich spor je však ještě o několik let starší. Oba muži se poprvé střetli již v roce 1994 na konferenci v Tucsonu v Arizoně. Koch, tehdy již velmi známý, tvrdil, že je vědomí vědecky dobře zvládnutelné a vysvětlitelné a dokonce prohlásil, že identifikoval možný základ vědomí, mozkové buňky aktivující se 40krát za sekundu. Mladší a tehdy méně známý Chalmers zásadně nesouhlasil. Tvrdil, že ani tyto 40 Hertzové osscilace, ani žádný jiný známý fyzikální proces nemůže vysvětlit, proč jsou vjemy doprovázeny vědomými procesy, například zdrcující nudou vyvolanou termíny užívanými řečníky konference.

Chalmers tehdy nazval vědomí těžkým problémem, což je termín používaný dodnes. Navrhl také, že problém by se dal vyřešit předpokladem, že informace je základní vlastností reality. To by mohlo vysvětlit vědomí v jakémkoliv systému, nejen v mozku. Takže třeba i neživé přístroje by mohly v principu disponovat jakýmsi vědomím. Kocha to příliš nezaujalo a v kuloárech na Chalmerse zaútočil. Jeho informační hypotézu označil za neověřitelnou, a tudíž bezcennou a prohlásil: „Proč neřeknete, že když máte mozek, sestoupil na vás Duch svatý a učinil vás vědomým?“ Následovalo několik let přenic, které vyvrcholily v roce 1998, když se oba pánové vsadili o bednu vína, že se do 25 let podaří najít jasný nervový vzorec, který je základem vědomí.

V průběhu let se Kochův postoj dramaticky změnil, když přijal informační teorii od italského neurovědce Giulia Tononiho. Ta je mnohem podrobnější než podobná hypotéza Chalmerse a tvrdí, že třeba i jediný proton by mohl mít jakýsi záblesk vědomí, protože v něm dochází k výměně informací mezi kvarky. Postoj Chalmerse se naproti tomu příliš nezměnil. V roce 2023 byla sázka vyřešena. Jak, to asi tušíte všichni, protože pokud máte jen základní povědomí o vědě mimo kosmonautiku, víte, že žádný zásadní průlom v oblasti vědomí nepřišel. Podmínky sázky přitom hovořily, že důkazy o nervovém popisu vědomí musí být jasné. A jak Chalmers řekl, je jasné, že zatím nic není jasné. Koch tedy prohrál a přinesl Chalmersovi jeho bednu s vínem jako výhru.

Ale spor zcela neskončil. Oba vědci se okamžitě vsadili znovu, opět na 25 let a tentokrát o dvě bedny vína. Koch vsadil, že v příštím čtvrtstoletí přijde jasný a zřetelný pokrok v oblasti vědomí a věci se vyjasní. Tedy, že do roku 2048 už jasný nervový vzorec, který je základem vědomí znám bude. V roce 2048 bude Kochovi 91 a Chalmersovi 82, takže je otázka, zda se výsledku vůbec dožijí. Chalmers řekl: „Nesmírně si přeji, abych tuto druhou sázku prohrál, ale obávám se, že vyhraju.“ Nezávislý vědecký komentátor John Horgan dodal, že se domnívá, že v roce 2048 bude situace kolem vědomí ještě více matoucí než dnes.

Kdy se první člověk dožije 150 let?

Velmi zajímavou sázku uzavřeli v roce 2000 Steve Austad a Stuart Jay Olshansky. Oba pánové se věnují problematice dlouhověkosti, Austad jako biolog, Olshansky jako lékař. Z toho důvodu uzavřeli sázku, zda se někdo narozený před rokem 2000 (tedy nejpozději 31. 12. 2000) dožije věku 150 let nebo vyššího. Sázka se pochopitelně rozhodně až v roce 2150. Přitom však Austadovi bylo v roce 2000 54 let, Olshanskému 46 let. Je tedy nad Slunce jasné, a to i jim oběma, že se rozhodnutí nemají šanci dožít. Jak je to tedy zařízeno? Podobně jako u výše jmenované sázky Freemana Dysona. Rozhodnutí se dožijí jejich potomci, takže potomek poraženého v sázce vyplatí výhru potomkovi vítěze.

Ještě zajímavější je fakt, že se Austad a Olshansky vsadili o částku v hodnotě 500 milionů amerických dolarů. Ano, čtete správně 500 milionů dolarů. Ani jeden z nich není podnikatel, jsou to vědci, kteří jsou v USA placeni sice relativně solidně, ale přesto takovou částkou ani jeden z nich nedisponuje. Ale i to mají vyřešeno. Každý z nich vsadil 300 amerických dolarů, které jsou však vloženy na speciálním fondu, a tak hodnota vložených peněz dosáhne v roce 2150 oněch 500 milionů dolarů. Potomek jednoho z vědců si tak možná bude moci užívat značného bohatství.

Matematický problém tisíciletí

V matematice existuje celá řada slavných nevyřešených problémů, za všechny jmenujme alespoň Goldbachovu hypotézu, Riemannovu hypotézu a problém P vs. NP, který bývá často označován za nejsložitější. Jde o to, zda jsou třídy složitosti P a NP totožné, tedy zjednodušeně o otázku, zda každý problém, u něhož počítač dokáže rychle ověřit správnost řešení, dokáže také počítač sám rychle vyřešit. Obecně se má za to, že existují problémy, u nichž je samotné řešení mnohem složitější než ověření platnosti řešení, a tedy P se nerovná NP, ale dosud to nikdo matematicky nedokázal.

A právě tento problém byl předmětem sázky mezi teoretickým informatikem Michaelem Sipserem a počítačovým vědcem Leonardem Adlemanem. Sipser v roce 1975 vsadil unci zlata na to, že problém bude vyřešen do roku 2000, zatímco Adleman sázel proti. Sipser prohrál, problém nebyl do konce století vyřešen, a proto poslal Adlemanovi jako výhru 2000 oficiálních amerických zlatých mincí American Gold Eagle.

Nutno dodat, že problém P vs. NP zůstává nevyřešen dodnes. Právě v roce 2000 jej Clayův matematický institut zařadil mezi jeden z problémů tisíciletí. Celkově je těchto problémů sedm a za vyřešení každého z nich je vypsána odměna milion amerických dolarů. Dalšími problémy jsou Hodgeova domněnka, Poincarého domněnka, Riemannova hypotéza, Yangova-Millsova teorie a hypotéza hmotnostních rozdílů, Navierovy-Stokesovy rovnice hydrodynamiky a Birchova a Swinnerton-Dyerova domněnka. Ze všech sedmi byla zatím dokázána pouze Poincarého domněnka (dnes již věta). Úspěšný řešitel, matematik Grigorij Perelman ji dokázal v roce 2006, avšak finanční odměnu a matematická ocenění s tímto spojená odmítl.

Prolomí kvantové počítače současné šifrování?

S výše uvedeným souvisí internetová bezpečnost a problém šifrování a faktorizace. Pokud by totiž P a NP byly rovny, internetová bezpečnost by byla ohrožena. Současné šifrování stojí na sytému RSA vyvinutém původně v roce 1973 britským matematikem Cliffordem Cocksem, avšak ten pracoval pro armádu, a tedy v utajení. Veřejně publikovali totéž v roce 1977 Ronald Rivest, Adi Shamir a Leonard Adleman (zmíněný o podkapitolu výše). Mimochodem, správně by se to mělo psát jako ARS, ale Adleman trval na tom, že na projektu odvedl nejméně práce, a tedy bude uveden až na třetím místě a od té doby známe sytém jako RSA.

RSA je šifra s veřejným klíčem. K šifrování potřebujeme dva klíče. Obvykle je jeden veřejný, ten je určen k šifrování zprávy, zatímco druhý je privátní a je určen k dešiforvání zprávy. Odesilatel zprávy ani nemusí znát privátní klíč pro dešiforvání a především, odesilatel a příjemce zprávy spolu nemusí sdílet žádné informace, čímž významně klesá riziko odhalení. Běžné metody, jako právě RSA, jsou založeny na tzv. jednosměrných funkcích, obvykle na faktorizaci neboli rozkladu na prvočísla. Využívá se toho, že když máme dvě velká prvočísla o délce několika stovek cifer, není zas tak těžké je vynásobit. Avšak složené číslo, které jejich vynásobením vzniklo je téměř nemožné rozložit zpět na původní prvočísla. Zatímco vynásobení zvládnou počítače během chvíle, rozklad na prvočísla trvá i stovky let.

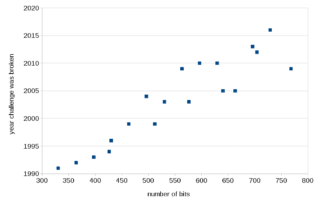
Existovala dokonce i soutěž v RSA faktorizaci, kdy bylo zveřejněno několik různě dlouhých složených čísel, které měli odborníci za úkol rozložit na prvočísla. Faktorizace prvního z nich, dlouhého sto číslic, trvala několik dní. Zatím nejdelší rozložené číslo má 250 cifer a jeho rozklad je ekvivalentní 2 700 rokům práce jednoho počítače. Ale není třeba se bát, když se rozkládají takto velká čísla? Není, jednak jde o výzvu pro nejlepší vědce, jednak tyto rozklady trvají poměrně dlouho a jednak stačí přidat pár dalších cifer a rozklad bude opět nemožný.

Největší zveřejněné číslo v této soutěži má 617 cifer a za jeho faktorizaci byla vypsána odměna 200 000 amerických dolarů. Zatím nikdo jej však rozložit na prvočísla nedokázal. V roce 2017 se kryptograf Francisco Rodríguez-Henríquez a matematik Daniel Bernstein vsadili, zda kvantové počítače způsobí revoluci v šifrování. Konkrétně šlo o to, zda kvantové počítače do roku 2033 prolomí právě faktorizační výzvu RSA-2048, tedy toto výše zmíněné číslo s 617 ciframi, což odpovídá 2 048 bitům. Uvidíme za 8 let.

Bratrovražedný souboj

Existenci antihmoty dokázali již ve 30.letech Carl Anderson a Seth Neddermayer, kteří našli pozitron, antičástici elektronu. Později se však vědci snažili najít i těžší antičástice, například antiproton (částice se stejnými vlastnostmi jako proton, jen se záporným elektrickým nábojem). Jeho hledání se věnoval například americký fyzik německého původu Gerson Goldhaber, který pracoval pro Lawrence Berkeley National Laboratory. Jeho bratr Maurice, rovněž částicový fyzik, byl však k práci svého sourozence skeptický, a proto se vsadil s kolegou o 500 dolarů, že Gerson antiproton nikdy nenajde, protože se domníval, že antiprotony ani neexistují. A prohrál. Z toho plyne ponaučení, že někdy není na škodu důvěřovat svým sourozencům.

Stejné chyby se ovšem dopustil i nositel Nobelovy ceny za chemii, fyzik Edwin McMillan, který byl společně s Glennem Seaborgem oceněn za výrobu prvního transuranu, prvního známého prvku těžšího než uran. Také McMillan vsadil 500 dolarů na to, že se antiproton nenajde. Ovšem jeho oponentem nebyl Gerson Goldhaber, nýbrž jeho kolega Emilio Segrè, fyzik italského původu. McMillan nejen, že prohrál, ale ještě motivoval Segrèho a jeho kolegu Owena Chamberlaina k tvrdší a rychlejší práci. Oba se totiž zatvrdili, a rozhodli se, že antiproton najdou. To se jim podařilo, a dokonce za to v roce 1959 obdrželi Nobelovu cenu za fyziku.

Jak se budou vyvíjet ceny komodit?

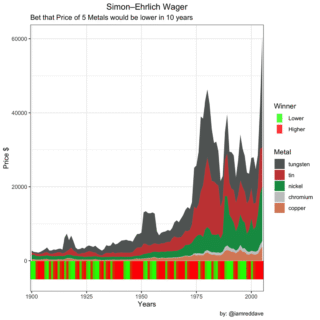
Snad nelze napsat článek o vědeckých sázkách a nezmínit patrně tu nejslavnější mezi biologem Paulem Ehrlichem a ekonomem Julianem Simonem. Je ovšem pravda, že právě o ní toho již bylo napsáno dost a dala by se navíc zpracovat do samostatného článku, takže jen stručně. Sázka byla motivována sporem o nedostatek zdrojů. Ehrlich totiž v roce 1968 knihu, v níž se věnoval populačnímu růstu a tvrdil, že se blíží demografická katastrofa, kdy lidstvo bude růst rychleji, než budou růst zásoby potravin a dalších zdrojů. Dokonce prohlásil, že kdyby si mohl vsadit, řekl by, že Anglie nebude v roce 2000 existoval.

Simon jako ekonom byl k těmto tvrzením velmi skeptický. Prohlásil, že vsadí 10 000 dolarů na to, že cena surovin nekontrolovaných vládou, a to včetně obilí, či ropy, v dlouhodobém horizontu nebude narůstat. Navrhl proto Ehrlichovi, aby si vybral libovolnou surovinu a libovolnou dobu delší než jeden rok a on s ním uzavře sázku, že po uplynutí této doby bude cena těchto komodit nižší než v době sázky. Ehrlich s kolegy vybral pět kovů – cín, chrom, měď, nikl a wolfram. Mysleli si totiž, že jejich cena výrazně poroste. Sázka byla uzavřena v září 1980 a to na dobu 10 let, tedy do září 1990.

Ehrlich a kolegové nakoupili od každého kovu množství za 200 dolarů, přičemž bylo dohodnuto, že pokud vzrostou, zaplatí Simon rozdíl mezi 1000 dolary a skutečnou cenou a naopak, pokud ceny klesnou Ehrlich a spol. zaplatí Simonovi. A jak to tedy dopadlo? Mezi roky 1980 a 1990 vzrostla světová populace o 800 milionů osob, to je největší do té doby zaznamenaný nárůst. Přesto však cena tří z pěti vybraných kovů nominálně klesla a v případě započtení inflace se dokonce snížila cena každého z pěti Ehrlichem vybraných kovů! A u některých dokonce poměrně výrazně. Ehrlich tedy vyrovnal Simonovi rozdíl ve výši 576 dolarů.

Tato sázka je z mnoha důvodu velmi poučná. Tak například se Ehrlich a Simon snažili dlouze dohodnout na druhé sázce, ale nikdy se jim to nepodařilo, každý měli totiž zcela odlišné představy. Ehrlich s kolegy dokonce navrhli novou sázku na 15 tehdy aktuálních trendů, jako jsou koncentrace ozonu v nižších vrstvách atmosféry, emise oxidu siřičitého v Asii, počet úmrtí na AIDS a podobně, přičemž chtěl vsadit 1 000 dolarů na to, že se každý z nich v průběhu následujících deseti let zhorší. Simon ovšem sázku nepřijal a zdůvodnil to následující analogií: „Předpovídám, a to je pravda, že průměrné výkony na příští olympiádě budou lepší než na té minulé. V průměru se výkony zlepšují, olympiádu od olympiády a to z různých důvodů. Ehrlich a další říkají, že nechtějí sázet na výkony, chtějí sázet na podmínky trati, funkcionáře, nebo jakékoliv jiné podobné nepřímé měřítko.“

Lze také argumentovat, že v případě sázky na ceny oněch pěti výše zmíněných kovů a to na stejnou dobu 10 let, ale v jiném období anebo sázky na delší dobu např. 1950–1975 nebo 1980–2011) by mohl vyhrát Ehrlich. Naopak se ukázalo, v opravdu dlouhém období 1934-2013 měla hodnota komodit výrazně klesající tendenci, a tedy by opět vyhrál Simon. Laické hodnocení ve smyslu, že ekonom Simon měl štěstí a biolog Ehrlich, který správně varoval před nebezpečím ekologické krize je tedy lákavé, ale nesprávné. Navíc se ukazuje, že původní Ehrlichovy texty nebyly zcela vědecky korektní.

Simon se v roce 1996 nakonec vsadil ještě jednou, tentokrát o 1000 dolarů s profesorem lesnické fakulty Auburnské univerzity Davidem Southem o to, že cena dřeva v následujících pěti letech klesne. Simon však v té době byl již dosti nemocný, nakonec zemřel roku 1998. Proto v roce 1997 Southovi předčasně vyplatil výhru 1000 dolarů, neboť očekával, že ceny dřeva zůstanou na hodnotě z roku 1996, což se nakonec také stalo.

Chyba či terorismus jako nástroj masové zkázy?

Na závěr se ještě vraťme k již dříve zmíněné stránce Longbets. Právě tam se totiž uskutečnily dvě zajímavé sázky, jimiž dnešní článek ukončíme. První uzavřeli britský královský astronom a držitel mnoha ocenění Sir Martin Rees a kanadský psycholog a psychoanalytik Steven Pinker. Šlo o tzv. bioerror nebo bioterror. Přesné znění sázky: „Bioerror nebo bioteror povede k jendomu milionu obětí (nebo více) v rámci jediné události během šestiměsíčního období počínajícího nejpozději 31. prosince 2020.“ A co že je ten bioerror a bioteror. Bioerror je nějaká chyba, například únik smrtícího viru z laboratoře, bioteror je použití biologických zbraní ať už ve válce či v rámci teroristického útoku.

Sázka byla uzavřena v roce 2017 a končila rokem 2020. Rees je známý svým skepticismem až pesimismem k rozvíjejícím se vědeckým technologiím, proto jimi argumentoval i nyní. Obával se prudkého nárustu schopností biotechnologií a jejich zneužitelností. Naopak Pinker argumentoval tím, že kognitivní zkreslení nafukuje scénář možné katastrofy a také tím, že pesimisté jsou obvykle vnímáni jako zodpovědní a seriózní, zatímco optimisté jako naivní, přesto je však většina předpovědí soudného dne chybná. Dále argumentuje i pravděpodobností ničivých událostí. Dohodnuto bylo, že počet obětí bude určen podle statistiky WHO, CDC nebo BPHS (podle toho, která organizace bude mít počet nejvyšší) a neměl by zahrnovat nepřímá úmrtí.

Zajímavé je, že tato sázka zůstávala dlouho nevyřešená. Důvod vás asi napadne – COVID-19. Ten totiž vypukl na konci roku 2019 a mnoho lidí spekulovalo o tom, že unikl z laboratoře v čínském Wuchanu. V tom případě by podmínky byly splněny a vyhrál by Rees. Samozřejmě je však laboratorní únik stále dost kontroverzní hypotéza. Proto byla stanovena dodatečná podmínka, že pokud alespoň dvě (v podmínkách jmenované) agentury, které se zabývají veřejným zdravím, prohlásí do konce roku 2024 původ viru SARS-CoV-2 ve Wuchanské laboratoři za velmi pravděpodobný, bude vítězem Rees. To se však nestalo, a proto byl nakonec za vítěze prohlášen Steven Pinker.

Zničí LHC planetu Země?

Na závěr si nemohu odpustit jednu sázku, kterou bych nazval vyloženě komickou, na odlehčení. A která také krásně ilustruje důležitost přesných podmínek, za nichž je sázka považována za splněnou. Tuto sázku uzavřeli v roce 2008 umělec Joe Keane a podnikatel a futurista Nick Damiano. Sázka byla uzavřena na deset let, do roku 2018 a výhra byla stanovena na 1000 dolarů. Přesné znění sázky zní takto: „Velký hadronový urychlovač (LHC) zničí Zemi.“

Jaké byly argumenty obou stran? Keane byl velmi stručný, podle něj je teoretická fyzika neúplná ohledně popisu procesů při vysokých energiích a tedy nevíme, co se stane. To Damiano byl výrazně sdělnější. Argumentoval vcelku pochopitelně částicemi vysokoenergetického kosmického záření schopnými dosahovat o mnoho řádů vyšší energií než LHC, tím, že hypotetická mikroskopická černá díra by se buď okamžitě vypařila Hawkingovým zářením anebo rostla jen velmi pomalu a podobně.

Damiano nicméně na závěr svého argumentu dodává.
„V nepravděpodobném případě, že:
a) LHC Zemi skutečně zničí
b) Lidstvo tuto událost přežije a přestěhuje se někam jinam do vesmíru
c) Já sám budu stále naživu
d) Příjemce výhry (dobročinná organizace vybraná Keanem) stále existuje
e) Peníze, jak je známe, stále mají hodnotu
Pak rád zaplatím. Zajímalo by mě, který ze scénářů podle pana Keanea zničí planetu.“

Velmi kuriózní jsou také podmínky v sázce dojednané. Znějí takto:
„Předpověď je správná, pokud je Země v důsledku provozu urychlovače částic LHC zničena, zredukována na mnohem menší objem než dříve, odpařena, rozbita na velké kusy, přeměněna na fotony, neutrina nebo jiný typ záření, přeměněna na exotickou hmotu, nebo prostě „jen“ není schopna udržet život. Pro účely sázky by Země měla být považována za zničenou, pokud v době konce trvání této sázky v roce 2018 nebudou na povrchu planety žít žádné lidské bytosti. Škody způsobené nepřátelskými bytostmi jsou zahrnuty, pokud jsou kauzálním důsledkem provozu urychlovače. Teleportace Země na jiné místo ve vesmíru, nebo do vesmíru alternativního, kde je stále schopna udržet život, je výslovně vyloučena. Sázka je vyhrána, pokud jakákoliv vědecká komunita, která v této době zbývá, ať už lidská, strojová nebo mimozemská, uzná, že zničení Země s největší pravděpodobností bylo důsledkem Velkého hadronového urychlovače, nebo jeho produktu (např. strangelet, mikroskopická černá díra a podobně).“

Závěr

Myslím, že článek je už tak dost dlouhý, nebudeme jej tedy ještě protahovat. Na závěr tedy snad jen tolik, že vědecké sázky jsou mimořádně zajímavé z mnoha různých důvodů. Mohou sloužit vysloveně pro pobavení, ale i k vyřešení závažných vědeckých či společenských otázek. Byť je samozřejmě otázka, nakolik jde sázejícím o pravdu a nakolik o ego či zviditelnění.

Použité a doporučené zdroje

• LongBets: https://longbets.org/
• Scientific wager na EN Wiki: https://en.wikipedia.org/wiki/Scientific_wager

Dále k přečtení

• Podrobněji o sázce Annan vs. Whitehouse: https://skepticalscience.com/print.php?n=1223
• Více o sázce Koch vs. Chalmer: https://www.scientificamerican.com/article/a-25-year-old-bet-about-consciousness-has-finally-been-settled/
• The Bet (Paul Sabin) – kniha o sázce Ehrlich vs. Simon: https://www.goodreads.com/book/show/17572998-the-bet

Zdroje obrázků

• https://i0.wp.com/www.science-shenanigans.com/wp-content/uploads/2017/09/Wagers-In-Science.png
• https://www.physics.muni.cz/astrohistorie/obrazky/kep_port.jpeg
• https://i2.wp.com/neomano.com/wp-content/uploads/2020/06/halley_hooke_wren.png
• https://cdn.mos.cms.futurecdn.net/3buDqF4oZrEByNRVBgYwmm-1200-80.jpg
• https://cdn.britannica.com/49/22949-050-5C717724/Alfred-Russel-Wallace-detail-photograph-painting-National.jpg
• https://upload.wikimedia.org/wikipedia/commons/a/a4/Cygnus_A_composite.jpg
• https://www.aavso.org/sites/default/files/images/baade.jpg
• https://upload.wikimedia.org/wikipedia/commons/e/eb/Stephen_Hawking.StarChild.jpg
• https://www.nasa.gov/images/content/604631main_cygnusx1_665.jpg
• https://www.societyforscience.org/wp-content/uploads/2019/08/thornekip_2015-Intel-STS-Awards-Gala-0304.jpg
• https://ep-news.web.cern.ch/sites/default/files/styles/full_image/public/2024-06/Preskill_Alta_May2020.jpg
• https://media.istockphoto.com/id/184100460/photo/gas-can.jpg?s=612×612&w=0&k=20&c=TCzvGTR1fYDWa9ZtJKES7YY3Ih96GfLsyo3O4qfwxXQ=
• https://i1.rgstatic.net/ii/profile.image/272834668789766-1442060262611_Q512/James-Annan.jpg
• https://upload.wikimedia.org/wikipedia/commons/0/04/Freeman_dyson.jpg
• https://seniorcorrespondent.com/wp-content/uploads/2021/02/PaulGilster.jpg
• https://scontent-prg1-1.xx.fbcdn.net/v/t39.30808-6/305029479_416073117176435_7223240516766229331_n.jpg?_nc_cat=110&ccb=1-7&_nc_sid=6ee11a&_nc_ohc=bzXxlaN2dL8Q7kNvwGEGm_l&_nc_oc=AdnDHmqrCI9bfDEO7HkkNAegOzqrOljKrXJDM6jWXJpajlByPgcnxm2-hvhjAQgGPYE&_nc_zt=23&_nc_ht=scontent-prg1-1.xx&_nc_gid=ba8iVbUISqUGLyIsyg5kCw&oh=00_AfP0sJhc6VRdFYN38AMPx9OHbrdgZ7ApeQtq4_tg5HO3nQ&oe=6864602D
• https://i1.rgstatic.net/ii/profile.image/327654625562624-1455130358050_Q512/Andrew-Burchill.jpg
• http://static.ddmcdn.com/gif/jwst-art-670×440-150421.jpg
• https://www.nasa.gov/sites/default/files/thumbnails/image/artemis_iii_report_graphic_crop.jpg
• https://cdn.mos.cms.futurecdn.net/Tp4fgfjWPaTwcp34Jt7J4E-1024-80.jpg.webp
• https://www.nbi.dk/~petersen/Physics/persons/feynman_gellmann2.jpg
• https://www.trinityremembered.com/biographies/imgs/Weisskopf.jpg
• https://images.computerhistory.org/chess/computer-chess.david-levy.102634530.jpg?w=600
• https://www.genome.gov/sites/default/files/media/images/2024-11/GeneSweep_graphsv2.png
• https://media.licdn.com/dms/image/v2/D4D10AQGJVwdig_v6rg/image-shrink_800/image-shrink_800/0/1721052823687?e=2147483647&v=beta&t=Kc9QFDZ1-nDm-ZWqgW71xx6Vq15Ygela80EKVZxiBQ0
• https://cpb-us-e2.wpmucdn.com/sites.uci.edu/dist/c/442/files/2012/12/MSSMBrokenEnglish.jpg
• https://upload.wikimedia.org/wikipedia/commons/thumb/8/8c/David_Gross_LANL.jpg/1200px-David_Gross_LANL.jpg
• https://alleninstitute.org/wp-content/uploads/2022/12/christof_koch_web-new.jpg
• https://upload.wikimedia.org/wikipedia/commons/thumb/f/fb/David_chalmers.jpg/1024px-David_chalmers.jpg
• https://cms.nmn.com/wp-content/uploads/2021/09/LONGEVITY.jpg
• https://i.ytimg.com/vi/ekxsnrVcYgc/sddefault.jpg
• https://i.pinimg.com/736x/85/c0/4a/85c04a7f0c52c7d1e55f4a448db5e38a.jpg
• https://www.esat.kuleuven.be/cosic/wp-content/uploads/2016/05/1.png
• https://media.springernature.com/lw685/springer-static/image/art%3A10.1007%2Fs00016-010-0040-7/MediaObjects/16_2010_40_Fig2_HTML.jpg
• https://i.redd.it/f4aa7xv1bt061.png
• https://s.wsj.net/public/resources/images/OB-YS375_bkrvth_P_20130829121516.jpg
• https://dl6pgk4f88hky.cloudfront.net/2021/06/barbaragibson_rees_and_pinker_final_1280x913-1038×778.jpg
• https://mzd.gov.cz/wp-content/uploads/2020/07/covid-19-4961257_1280.jpg
• https://home.cern/sites/default/files/2022-03/0807031_01-a4-at-144-dpi-min.jpg
• https://blog.sciencemuseum.org.uk/wp-content/uploads/2013/07/alien-cartoon-high-res1.jpg