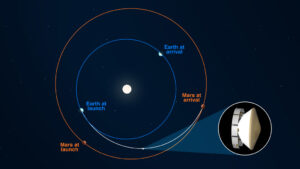
V úterý ve 21:40 SEČ mohlo pozemní středisko zodpovědné za vozítko perseverance vydat zprávu, která oznamuje, že sestava projektu Mars 2020 urazila od startu 30. července už 235,4 milionu kilometrů. Přesně stejná vzdálenost přitom v danou chvíli ještě zbývala do chvíle, než pouzdro se složeným vozítkem vletí rychlostí 19 000 km/h do atmosféry Marsu, k čemuž dojde 18. února 2021. „Nemyslím si sice, že by nám za tenhle milník někdo upekl dort, zvlášť když teď většina z nás pracuje z domova, ale je to příjemný milník. Další zastávka – kráter Jezero,“ uvedla Julie Kangas z JPL, která se na misi podílí v pozici navigátora.
Zdroj: https://www.nasa.gov/
Gravitační vliv Slunce velmi významně ovlivňuje oběžné dráhy v celé soustavě a ani přeletová dráha od Země k Marsu není výjimkou. Inženýři musí při plánování dráhy počítat i s pohybem obou planet v průběhu letu. Z těchto důvodů je přeletová dráha zahnutá a nikoliv rovná jako přímka. „Urazili jsme sice poloviční vzdálenost, kterou musíme k Marsu doletět, ale nejsme v poloviční vzdálenosti mezi oběma planetami. Pokud bychom nakreslili přímou spojnici, pak je Perseverance 42,7 milionu kilometrů od Země a Mars se nachází 28,8 milionů kilometrů před ním,“ vysvětluje Kangas.
Za tohoto stavu trvá signálu jednosměrná cesta od sondy k Zemi (případně opačným směrem) 2 minuty a 22 sekund. Celkem má cesta roveru Perseverance k Marsu měřit 470,8 milionu kilometrů a v době přistání bude rudá planeta vzdálena od Země 209 milionů kilometrů – signálu tak bude cesta trvat 11,5 minuty. Pozemní tým zatím stále kontroluje stav všech palubních systémů. 15. října byla ověřena funkce přístrojů RIMFAX a MOXIE – v obou případech se zdá, že fungují správně. 19. října přišla dobrá zpráva týkající se správného fungování přístroje MEDA a 16. října zbýval už jen poslední úkol z řady zkoušek přístroje PIXL.
„Pokud nějakou částí našeho roveru protéká elektřina, chceme si ověřit, že daná část funguje i po startu správně,“ říká Keith Comeaux, zástupce hlavního inženýra mise Mars 2020 a dodává: „Díky těmto kontrolám prokládaným nabíjením akumulátorů vozítka i vrtulníku, uploadováním složek a sekvencí pro povrchové činností, nebo plánováním a vykonáváním korekčních manévrů máme harmonogram naplněný až do přistání.“
Přeloženo z:
https://www.nasa.gov/
Zdroje obrázků:
https://www.nasa.gov/sites/default/files/thumbnails/image/1-pia24231-1041.jpg
https://www.nasa.gov/sites/default/files/thumbnails/image/2-pia24232-1041.jpg






Škoda že mu vybrali názov Perseverance. Má jazdiť po Jazere, tak by sa hodil názov s lodnou tematikou, napríklad Křižník.
Ako vlastne Američania vyslovujú Jezero?
Velmi často se setkávám s výslovnosti džezerou / džezero.
Hlavně, oni v naprosté většině nevědí, co slovo Jezero znamená.
Dobrý den,
můžete mi říct jaká je pravděpodobnost, že se vozítko po cestě srazí s nějak kosmickým tělesem nebo smetím?
Děkuji.
PavelZ
Hezký den,
je to velmi nepravděpodobné. Zatím se to ještě nestalo. Kosmické smetí v těchto oblastech prakticky neexistuje.
Děkuji.
pavelZ
Hned první sonda k jiné planetě – Mariner 2 – dvakrát ztratila orientaci a na vině měl být v obou případech mikrometeorit. Také u ruských sond k planetám, které ztratili těsnost, příkladně Mars-5, mohl být příčinou mikrometeorit.
Tak mikrometeoridy jsou něco jiného. Tazatel se ptal na kosmická tělesa, což je pro mne označení větších objektů, které už mohou způsobit nějakou znatelnou škodu. A kosmické smetí (druihá část dotazu) jsou produkty lidské činnosti, takže ani v tomto případě o mikrometeoroidy nejde.
Mikrometeorit nebyl správný termín, v případě Marineru, pokud tomu tak bylo, se jednalo o větší tělísko, dostatečně hmotné aby roztočilo kosmickou loď o váze 2 metráků. Totéž platí pro ruské sondy, mikrometeorit by byl malý, stěnu sondy by neprorazil.
Pokud se týče kosmického smetí mohou se s ním sondy setkat po startu, po odhození AE krytu, kdy zpravidla vyčkávají na parkovací dráze a poté při odletu, vše probíhá v prostoru, kde je nejvíce k.smetí.
Myslím, že tohle se řešilo někdy před padesáti lety, kdy se chystal první průlet pásem planetek mezi Marsem a Jupiterem (Pioneer 10). Nevědělo se, jaká je tam hustota materiálu. A další případ je třeba Cassini, která musela během brzdného manévru proletět těsně kolem Saturna, kde jsou shodou okolností prstence. Takže byla nucena dvakrát proletět jejich rovinou, jednou z jejích mezer. Tady bylo riziko určitě reálnější. Ta mezera je sice široká 26 000 km, ale uvnitř se samozřejmě najde materiálu dost a Cassini to také mnohokrát schytala (pokud vím, tak snad až 100 000 krát), naštěstí jen od skutečné drobotiny. Ale nedalo se nic dělat, musela do toho jít po hlavě 🙂
To je dobrá otázka, ale neexistuje na ni úplně jednoduchá odpověď. Ponechám stranou slovíčkaření, co nazývat mikrometeoroidem a co už „kosmickým tělesem“. Dejme tomu, že se otázka týkala obecně meteoroidů.
Už od 60. let vyvýjí NASA tzv. Meteoroid Enginineering Model. Ten popisuje hustoty, velikostní rozdělení, rychlostní a dráhové rozdělení meteoroidů v různých částech Sluneční soustavy a jeho primární účel je zhodnocení rizika zásahu kosmických sond nějakým takovým tělískem.
Vstupními údaji pro konstrukci takového modelu jsou jednak pozorování meteorů ze Země a jednak detekce nárazů meteoroidů pomocí k tomu určených detektorů, kterými byly vybaveny některé meziplanetární sondy.
Ten model prošel dlouhým vývojem a úpravami, v poslední době mu byla věnována velká „péče“ např. i kvůli vývoji dalekohledu Jamese Webba, který bude mít nechráněné hlavní zrcadlo.
Ale k Vaší otázce. Tu lze zodpovědět pouze tehdy, pokud ji formulujeme trochu přesněji, a sice, jaká je pravděpodobnost, že se Perseverance na své cestě srazí s meteoroidem _určité hmotnosti_ (nebo velikosti). Meteoroidy ve Sluneční soustavě (i asteroidy, tedy ta větší tělesa) jsou totiž velikostně rozděleny tak, že těch největších je málo a čím jdeme k menším rozměrům, tím jejich počty přibývají. Šance na srážku s menším meteoroidem je proto samozřejmě vyšší, na druhou stranu čím menší těleso, tím menší následky taková srážka bude mít.
Položme tedy otázku např. takto: Jaká je pravděpodobnost, že se Perseverance srazí s meteoroidem o hmotnosti 1 gram nebo větším (při typické srážkové rychlosti v oblasti kolem Země či Marsu, která je okolo 20 km/s, bude mít tělísko o hmotnosti 1 g kinetickou energii srovnatelnou s osobním automobilem uhánějícím po dálnici, což už lze určitě pro sondu považovat za fatální).
Meteoroid Enginineering Model říká, že 1 metr čtvereční povrchu sondy obdrží zásah takovým tělískem řádově 10^-7krát za rok. Když to přepočítáme na celý povrch pouzdra sondy (cca 30 m čtverečních) a dobu, kterou sonda k Marsu poletí (0,6 roku), dostaneme zhruba 2*10^-6 takových srážek za celou dobu letu, jinak řečeno pravděpodobnost srážky (za celou dobu letu) je 1:500000.
Stejný výpočet můžeme provést pro meteoroidy menších velikostí, kterých je mnohem více. Pro zásah meteoroidem o hmotnosti 1 miligramu vyjde pravděpodobnost za celou dobu letu na 1:50, a pro zásah meteoroidem o hmotnosti 1 mikrogramu to vychází na 20 takových srážek za celý let.
Díky za údaje!
pane Scheirichu,
díky za obsáhlou a fundovanou odpověď.
Snad k žádné kolizi nedojde, přistání se podaří a budeme se tak moct těšit, co nového Perseverance objeví.
pavelZ
Podobně jsou na tom i sonda čínská a arabská. V únoru bude u Marsu opravdu živo. K pracujícím družicím přiletí další dvě a na povrchu k pracujícímu landeru další jeden a pracujícímu roveru další dva.
Možno hlúpa otázka,
prečo je zvolená takáto dlhá trajektória, viem že sa štartovalo ku koncu štartovacieho okna, ale aj tak…470mil km ? S ľudskou posádkou to vyzerá na podobne dlhú trajektóriu. Prečo sa vlastne volí takáto predĺžená ? Nikdy sa neuvažovalo s kratšou misiou? Skrátka že na Mars by sa vyštartovalo popredu…teda skôr ako sa Mars dostane do najbližšej pozície, čiže by sme mu vlastne leteli „oproti“, pobyt na Marse by bol krátky..10-30dní..a nastal by odlet na zem a vlastne by sme zem „dobiehali“. Skrátka celá misia povedzme v 1/3 obehu Marsu okolo zeme neprešlo by sa najvzdialenejším miestom obehu. Možno sa pýtam hlúposť, ale viem že niektoré sondy to na Mars stihli skôr.
Všem sondám, které mají Mars jako svůj cíl, trvá přelet Země – Mars něco kolem 8 měsíců (+/- nějaký ten týden). Tato dráha (tzv. Hohmannova elipsa) se volí, jelikož je energeticky nejvýhodnější. Vámi navrhovaný postup (vlastně taková varianta čelní srážky) má zásadní problém v tom, že by byl energeticky nesmírně náročný. Především byste k Marsu přiletěl s mnohem větší rychlostí, které byste se nějak musel zbavit – buďto motorickým brzdícím manévrem (ohromná spotřeba paliva), nebo brzděním o atmosféru (extrémní tepelné namáhání). Obě varianty jsou mimo technické možnosti současné techniky.
Pokud vyjde okno na nejvhodnější polohu obou planet, dá se bez problému doletět k Marsu za čtyři měsíce. Předvedl to názorně Mariner-7. Startoval na Mysu 27.3.1969 a u Marsu byl již 5.8.1969, což jsou čtyři měsíce a pět dní, nebo přesně 127 dní.
Bylo to tím, že Mars byl v době příletu v periareu a sonda překonávala vzdálenost cca 40 mil km mezi drahami obou planet. Pokud je Mars v době příletu v apoareu, jako je tomu letos, musí sonda překonat cca 100 mil km mezi drahami obou planet a trvá to 8 měsíců.
Apoapsida a periapsida těles obíhajících okolo Slunce (což je případ Marsu) se nazývá perihel (perihélium) a afel (afélium). Periareum a apoareum jsou body oběžné dráhy okolo Marsu.
O.K. mám v těch názvech zmatek. Doufá, že to základní sdělení mého příspěvku, že se dá letět k Marsu 4 měsíce běžnou rychlostí bez dalších nároků.
Hezky je to popsané zde:
https://kosmonautix.cz/2014/03/menime-prehledne-rychlost-na-obezne-draze/
Takže sa dá celá výprava skrátiť na 8-10 mesiacov, problém je „ubrzdiť“ ?. Neviem ci to chápem správne ale rýchlosť obehu zeme okolo slnka ja cca 30 km/s. Mars obieha cca 25km/s…takže už tu je rozdiel cca 5km/S plus teda rýchlosť lode smerujúcej k Marsu cca 12km/s ? Potrebujem teda spomaliť z cca 17km/s. Nie je možný dáky oblet Marsu, „gravitačný manéver“ čo by lodi pomohol spomaliť. Nestojí skrátenie misie za zložitejšie technické riešenie ? Mám pocit že palivo môžme dotankovať na obežnej dáhe a štartovať až odtiaľ. Celú misiu začať z obežnej dráhy. Samozrejme dakde bude háčik,inak by tak lietala aj NASA…ale kde…je to v tom zabrzdení a pristáti ?
Palivo bychom teoreticky mohli doplnit na oběžné dráze, ale bylo by ho potřeba příliš mnoho. Ve vesmíru není tření, které by družici brzdilo. Co motorem urychlím, to motorem musím ubrzdit. Potřeboval bych tedy navíc palivo na brždění. To bych musel urychlovat dalším palivem. A všechno to palivo vynést ještě dalším palivem. Plus samozřejmě hmotnost nádrží. Tady je vidět, co způsobuje logaritmus v Ciolkovského rovnici. Řešení by bylo extrémně nákladné a cena nevyváží zisk z kratší doby přeletu.
Na gravitační manévr nemáme po cestě vhodné těleso, se kterým by si družice vyměnila kinetickou energii.
Dušan to sepsal dobře hned v první odpovědi. Hohmannova dráha je v současnosti optimální řešení.
Otázka vůbec není hloupá, jen odpověď není jednoduchá. Proto ji hledají všechny kosmické agentury.
Já možná tazateli doporučím hru Kerbal Space Program. V ní se člověk snadno a rychle naučí zákonitosti nebeské mechaniky, jak fungují manévry a tak dále. Doporučuji ji všem zájemcům o proniknutí do tématu.
A myslím, že to vobec nebola hlúpa otázka
patrí pánu Trúdovi
Super článok. Ten čas letí.. 🙂
Píšem kvôli chybe v druhom odseku. Čísla majú byť asi bez desatinnej čiarky. Teda 427 a 288 mil. km.
Kdepak, takhle je to správně. Teď jsem to ještě kontroloval na webu NASA. 😉