Pro dosažení i nejbližších hvězd je potřeba zajistit odpovídající pohon. Pokud půjde o raketový motor, je třeba zajistit nejen dostatek energie, ale také hybnosti, která zajišťuje zrychlování kosmické lodi. Let rakety a potřebné parametry popisuje Ciolkovského rovnice. Podívejme se na výzvy spojené s mezihvězdným letem, které nám ukazuje.

Na Oslovi i kosmonautixu jsem publikoval několik rozborů o možnosti mezihvězdných letů. Již v roce 2007 vyšla úvaha, zda je možná mezihvězdná expanze lidstva, v roce 2008 se rozebíraly jaderné zdroje, které jsou jediné schopné dodat dostatek energie pro vesmírnou kolonizaci a v roce 2013 byla snaha rozebrat, zda je možná hvězdná budoucnost lidstva. Pro dosažení rychlostí nutných k opuštění Sluneční soustavy lze ještě využít gravitačního praku nebo metodu sluneční plachetnice. Hypoteticky by se možná dala využít exotická fyzika za Standardním modelem hmoty a interakcí ve formě černých děr či warpu, ale to může být úplně mimo fyzikální realitu.

Ovšem klíčovými by měly být raketové motory. Podívejme se tak na zásadní problémy v této oblasti. Pokud chceme změnit rychlost kosmické lodi raketovým motorem, potřebujeme k tomu nejen dostatek energie, ale také hybnosti vyvrženého materiálu. Potřebné parametry a let rakety pak popisuje tzv. Ciolkovského rovnice. V následujícím článku jsem se pokusil rozebrat podmínky pro realizaci mezihvězdných letů z tohoto hlediska, přidal jsem řadu grafů, čísel i vzorečků. Doufám, že se najdou čtenáři, pro které bude i takto doplněný a detailnější článek zajímavý a užitečný.

Posuzované příklady mezihvězdných letů

Hvězdy jsou od nás ve srovnání s našimi současnými možnostmi cestování v obrovských vzdálenostech. Let k nim představuje extrémní výzvu. Je tak pochopitelně otevřenou otázkou, zda a kdy lidstvo tuto překážku překoná. Vzdálenosti nejbližších hvězd jsou větší než čtyři světelné roky. Tedy i světlo, které definuje hraniční rychlost v našem vesmíru, potřebuje k překonání těchto vzdálenosti roky. Pokud chceme mezihvězdný let realizovat v průběhu lidského života, tedy v řádu desetiletí, musí se naše kosmická loď pohybovat nejméně v řádu desítek procent rychlosti světla. Pokud chceme realizovat let trvající řádově staletí, potřebujeme dosáhnout nejméně procenta rychlosti světla.

Předpokládejme, že chceme dostat k nejbližším hvězdám automatické sondy. Jejich přežití v řádu staletí je sice velmi náročné, ale ne nepředstavitelné. Zároveň má lidská civilizace zkušenosti s realizací projektů trvajících staletí. Takže i takto dlouhé doby letu nejsou pro nás úplně mimo realitu. Takový mezihvězdný let se uvažuje i v čínské sci-fi Problém tří těles. Je pochopitelně otázka, jak zajistit, aby vědecké poznatky získané a odvysílané až po takové době nebyly v době dokončení projektu úplně morálně zastaralé. Diskuzi tohoto problému si necháme pro některý z příštích článků. Nyní se podíváme na problematiku čistě z hlediska energetické náročnosti a řešení Ciolkovského rovnice.

Nároky, které musí pohony mezihvězdných plavidel naplnit, si tak ukážeme na několika příkladech. Nejbližší hvězdou je Proxima Centauri, což je rudý trpaslík gravitačně vázaný k systému dvou hvězd slunečního typu Alfa Centauri. Vzdálenost tohoto systému od Země je zhruba 4,3 světelných let. Proxima Centauri má jednu potvrzenou exoplanetu zhruba hmotnosti i velikosti Země a dva kandidáty na exoplanety. Jeví se tak jako velmi zajímavý cíl první mezihvězdné výpravy.

Podrobněji rozebereme lety, kdy se dosáhne rychlosti 0,2 rychlosti světla, tedy 0,2 c, a o řád pomalejší, kdy nám bude stačit rychlost pouhých 0,02 c. V prvním případě se let realizuje v době překračující 22 let. Konkrétní doba letu závisí na tahu motorů a jak rychle se rychlosti 0,2 c dosáhne. Případně, jestli předpokládáme průlet touto rychlostí systémem Proximy Centauri nebo budeme při příletu k němu brzdit. V případě, pokud budeme zrychlovat do poloviny cesty konstantním zrychlením a pak zase konstantním zrychlením zpomalovat, bude doba trvání letu necelých 44 let. Je tak třeba počítat s dobou mezi 22 až 44 lety. Což už jsou doby srovnatelné s trváním současných dlouhodobých misí.

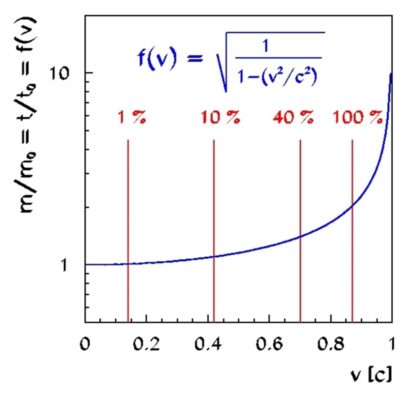
Je třeba připomenout, že i pro rychlost 0,2 c je pořád ještě možné využít nerelativistické přiblížení. Jak je vidět na grafu 1, až do rychlosti 0,14 c nepřekračuje rozdíl mezi relativistickým výpočtem a nerelativistickým klasickým přiblížením 1 %.

V případě rychlosti 0,02 c, která už je snáze dosažitelná, se už doba trvání mise protáhne na více než 200 let. To bude druhý námi podrobně studovaný případ. Budeme se hlavně věnovat těmto dvěma rychlostem. Pro srovnání pak ještě na opravdu relativistickou rychlost 0,8 c a poměrně nízkou rychlost 0,002 c (600 km/s), což může být již relativně brzy v našich technických možnostech.

Budeme předpokládat, že čistá hmotnost lodi po vypotřebování veškeré hmoty vyvrhnuté při urychlování či zpomalování lodi, bude 100 tun. Jen část z toho je užitečné zatížení, je zde také hmotnost motorů a dalšího vybavení potřebného k realizaci pohybu lodi. Hmotnost je vybrána tak, aby pro automatický let představovala realistickou hodnotu. Zároveň se pak dají získané hodnoty snadno přeškálovat pro řádové zvýšení či snížení hmotnosti lodi.

Možné typy pohonů

Než se podíváme na možné typy pohonů, připomeňme si fyzikální veličiny definující jejich parametry. Jedná se o tah motoru, specifický impuls a výtoková rychlost. Tah motoru udává sílu, kterou působí na urychlovanou loď, jeho jednotkou je newton. Udává, jaké zrychlení je schopen pohon poskytnout, a jak rychle se bude loď s danou hmotností zrychlovat. Na něm závisí, kdy dosáhne cílové rychlosti.

Specifický impuls je poměr tahu a hmotnosti spotřebované pracovní látky za časovou jednotku. Síla je spojena se změnou hybnosti za časovou jednotku a specifický impuls je tak, pokud se udává v jednotkách SI, roven efektivní výtokové rychlosti. Jako standard pro srovnávání si uveďme, že výtoková rychlost klasického raketového motoru využívající spalování kapalného vodíku je zhruba 4,5 km/s a jeho specifický impuls je tedy 4,5 kN s kg^-1.

Efektivní výtoková rychlost je přesně ta veličina, kterou lze využit ve zmíněné Ciolkovského rovnici. Rozdíl mezi skutečnou a efektivní výtokovou rychlostí je dán její transformací přes hybnost do tahu.

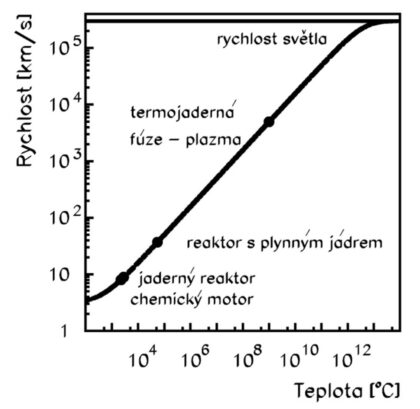
Potřebné výtokové rychlosti lze dosáhnout dvěma způsoby. První možností jsou tepelné motory. Zde je vysoká teplota spojena se střední kinetickou energií spojenou s chaotickým tepelným pohybem částic plynu nebo plazmatu. Dosažené teplotě odpovídá dosažená výtoková rychlost (viz graf 2). V tomto případě je kritická dosažená teplota. K jejímu dosažení lze využít například štěpné jaderné reaktory. V tomto případě se využívá vysokoteplotní reaktor s vysokým obohacením jaderného paliva. Ten ohřívá vodík, který je pracovní látkou. Ta pak vytéká tryskou ven. Jiné pracovní látky se také uvažovaly, ale ty měly i vzhledem k vyšším hmotnostem atomů nižší dosažitelné výtokové rychlosti.

Vysokoteplotní reaktory umožňují teploty v řádu 1000 ˚C. To je srovnatelné s motory využívající chemické hoření. V tomto ohledu se sice dosahuje vyšších efektivních výtokových rychlostí, než je tomu u raketových motorů na pevná paliva i těch na kapalná. Například jaderný reaktor projektu NERVA umožňoval teploty okolo 2 200 ˚C a efektivní výtokové rychlosti 8 km/s. Dalším vyladěním parametrů, včetně zvýšení teploty až ke 2600 ˚C, se lze dostat až k efektivní výtokové rychlosti blízké 10 km/s. To je dvojnásobné oproti raketovým motorům spalujícím vodík a kyslík.

Ještě vyšší teploty lze získat, pokud se kinetická energie neutronů vznikajících při štěpení předává přímo protonům vodíku. V tomto případě je potřeba mít úplně jinou konstrukci reaktoru. Musí se realizovat tekuté nebo plynné jádro obsahující štěpné palivo. V takovém případě by se v principu mohlo dosáhnout reaktory s plynným jádrem výtokové rychlosti až 40 km/s. Ovšem žádný prototyp takového reaktoru zatím nebyl realizován a jedná se o velkou technologickou výzvu.

Je ještě jedna možnost, jak pomocí štěpení získat větší výtokové rychlosti. Už na počátku kosmické éry se uvažovalo o využití jaderných explozí, které by se během letu postupně odpalovaly. Připomeňme projekt Orion i mezihvězdný let z čínské sci-fi Problém tří těles. Zde se dá dosáhnout vyšších výtokových rychlostí až 100 km/s. Ještě vyšší lze získat ve výbuších termojaderných bomb.

V případě využití termojaderné fúze lze dosáhnout daleko vyšších teplot, než je tomu u štěpení. Zde existují různé možnosti udržení plazmatu, a tedy i konstrukce termojaderného fúzního raketového pohonu. Je možné zkombinovat dlouhé udržení plazmatu a jeho relativně nízké hustoty v případě magnetického udržení nebo krátkou dobu udržení a velmi vysoké hustoty plazmatu udržení inerciálního. Podrobněji jsou různé možnosti realizace termojaderné fúze a současný stav v této oblasti popsány v nedávném článku, v dalším se popisuje nedávný rekord dosažený na čínském tokamaku. I z těchto rozborů je jasné, že zatím se nám fungující fúzní zařízení na Zemi vytvořit nepodařilo. Dosažitelné efektivní výtokové rychlosti závisí na využité reakci, dosažených teplotách a konkrétní využité metody udržení plazmatu i konstrukce reaktoru a motoru. Fúze by však mohla zajistit efektivní výtokové rychlosti v řádu stovek i tisíců km/s.

K ještě vyšším výtokovým rychlostem by mohlo pomoci využití antihmoty a anihilace. Nejdříve by v malém objemu mohla přispět k vylepšení fúzních pohonů a zvýšení dosažených teplot i výtokových rychlostí. V případě anihilačního pohonu by se pak výtokové rychlosti mohly blížit k rychlosti světla. O tom, jaká by mohla být reálná konkrétní konstrukce anihilačního pohonu však zatím představu nemáme a jejich konkrétní efektivní výtokové rychlosti jsou pouze spekulace. Připomeňme, že antiprotony (antinukleony obecně) anihilují s protony (nukleony) za vzniku mezonů. Ty nabité se rozpadají na miony a neutrina a neutrální pak na dva fotony. Anihilace elektronu a pozitronu vede také k produkci páru fotonů. Pokud jsou pracovní látkou fotony s rychlostí světla, dostaneme kosmickou loď, která se často označuje jako fotonová raketa. Ovšem reálný průběh anihilace a formování směru výletu pracovní látky je velkou otázkou a také extrémní technologickou výzvou. Fotony se dají produkovat i jiným způsobem, než je anihilace. Lze v principu využít i laser či fúzi, ale problémem u nich je malá účinnost konverze energie. Tedy, kromě toho, že fúzní zdroje nemáme a odpovídající lasery také ne.

Druhou možností jsou iontové motory, kde je výtoková rychlost dána uspořádaným pohybem iontů urychlených elektrostatickým, kombinaci elektrického a magnetického pole nebo vysokofrekvenčním elektromagnetickým polem. Existuje celá řada různých typů těchto pohonů. V tomto případě je zdroj energie využíván pro produkci elektřiny a ta se následně využívá pro napájení urychlovacího systému iontového motoru. Je třeba zdůraznit, že v tomto případě je efektivita využití energie dána konverzí vzniklé tepelné energie na elektrickou. Připomeňme, že u štěpných jaderných reaktorů, a podobné tomu bude u těch fúzních, je účinnost konverze mezi 30 až 40 %. Další i řádové ztráty energie jsou spojeny s fungováním iontového motoru. Urychlovat elektrickým polem lze pouze nabité ionty, ty je pak třeba po urychlení neutralizovat. Jak proces urychlení, tak i neutralizace iontů a řada podpůrných systémů vede k energetickým ztrátám. Většinou pak s růstem dosahované kinetické energie urychlených iontů tyto ztráty rostou. V další diskuzi musíme mít existenci těchto ztrát energie stále na paměti, i když se tam explicitně nebude zmiňovat.

V současné době využívají vesmírné iontové motory pro dodávku elektřiny fotovoltaické panely. Jde o elektrostatické typy motorů, které mají nízké tahy, tedy s nízkými intenzitami svazku urychlených iontů. Pro případné lety na velké vzdálenosti budou pravděpodobně využity systémy s vysokými tahy, jako je systém VASIMR.

Podívejme se na výtokové rychlosti iontových motorů. U těch současných se urychlují většinou ionty xenonu, ale využívá se i argon nebo jód. Je několik sond, které využily iontové motory. K planetce Psyche letí od 13. října 2023 stejnojmenná sonda, která využívá čtyři Hallovy iontové motory SPT-140. Ty mají výtokovou rychlost okolo 18 km/s a pomohou zrychlit její cestu k cíli i realizaci potřebných manévrů a změn dráhy. U využívaných iontových motorů se výtokové rychlosti pohybují mezi hodnotami 10 a 80 km/s. Testovány, i s využitím vakuové komory, už byly i pokročilé systémy s výtokovými rychlostmi 210 km/s.

Předpokládá se, že by se dalo dosáhnout až hodnot v řádu 10 000 km/s. V takových případech je však kritické, pro jaké by to bylo tahy motoru a účinnosti konverze elektrické energie na kinetickou energii urychlených iontů. Jak blízko se lze v budoucnu k této hodnotě inženýrsky dostat u reálně fungujícího motoru, je otázka úplně otevřená. Je možné zmínit, že urychlovače iontů dokážou tyto urychlit na rychlosti i extrémně blízké rychlosti světla. Ovšem intenzity svazku jsou extrémně malé a stejně tak účinnosti konverze energie při urychlování.

Potřebná kinetická energie

Než se s využitím diskutovaných výtokových rychlostí podíváme na Ciolkovského rovnici, připomeňme si energetické potřeby mezihvězdných letů. Hmotnost je spojená s energií světoznámou Einsteinovou rovnicí E = mc². Během exoergických jaderných reakcí se část klidové energie spojená s klidovou hmotností přemění na kinetickou energii. Při štěpení se uvolní zhruba 200 MeV energie a klidová energie uranu, který se štěpí, je zhruba 219 000 MeV. Na kinetickou energii se tak přemění zhruba 0,09 % klidové energie (stejný podíl hmotnosti). Hmotnost rozštěpeného uranu tak bude zhruba 1100krát větší, než je hmotnostní ekvivalent potřebné kinetické energie. Je třeba zdůraznit, že v každém štěpení vznikají různé produkty, takže se uvolněná energie při konkrétních štěpeních liší a je také rozdíl u různých štěpných jader. Zmíněných 200 MeV je tak přibližná hodnota.

U vesmírných fúzních pohonů se s největší pravděpodobností bude využívat reakce deuteria a helia 3, při které se uvolňuje 18,3 MeV. Součet klidový energií deuteria a helia 3 je 4 684 MeV. Na kinetickou energii se tak při této fúzní reakci přemění 0,39 % klidové energie (stejný podíl hmotnosti). V tomto případě tak musí být celková hmotnost deuteronu a hélia 3 jen 256krát větší, než je hmotnostní ekvivalent potřebné kinetické energie.

V případě anihilace proběhne v konečném důsledku přeměna veškeré zúčastněné hmoty a antihmoty na fotony a neutrina, tedy klidová energie se úplně přemění na kinetickou.

Nyní se podívejme, jaké jsou potřeby kinetické energie v našem případě urychlení kosmické lodi o hmotnosti 100 tun na rychlosti 0,2 c a 0,02 c. Jak bylo ukázáno, s přesností lepší, než jsou nízké jednotky procent, můžeme využit klasický vztah mezi kinetickou energií a rychlostí. U něj kinetická energie roste s kvadrátem rychlosti (E_K = (mv²)/2). Pokud vyjádříme rychlost v jednotkách rychlosti světla, můžeme vyjádřit kinetickou energii jako polovinu klidové energii lodi vynásobené kvadrátem její rychlosti v jednotkách rychlosti světla (E_K = ((mc²)/2)∙(v/c)². Klidová energie, která se tak musí přeměnit pro získání této kinetické energie je v případě rychlosti 0,2 c hodnota 2 tuny a v případě 0,02 c je to 0,02 tuny, což je 20 kg. Je však třeba připomenout, že se kinetická energie předává i pracovní látce zajišťující urychlení lodě. Reálně je tak potřeba energie vyšší, než je konečná kinetická energie lodi.

Jak to je s našimi různými možnostmi uvolňování energie. V případě využití pohonu na bázi antihmoty by stačilo anihilovat v případě rychlosti 0,2 c celkově dvě tuny hmoty a antihmoty, pro případ rychlosti 0,02 c jen 20 kg. V tomto případě je hmotnost paliva pro dodávku energie menší, a v případě menší rychlosti dokonce významně menší, než je hmotnost urychleného vesmírného plavidla. Připomínám, že zde absolutně neřešíme extrémní problémy s uchováváním antihmoty a konstrukcí motoru na antihmotu. Řešení toho je v nedohlednu. Neřešíme také, že část energie uniká ve formě neutrin a existuje celá řada dalších ztrát.

U fúzního pohonu už pro rychlost 0,02 c je potřeba 5,12 tuny sumární hmotnosti deuteria a helia 3, pro rychlost 0,2 c pak hmotnost 512 tun. V druhém případě už je hmotnost tohoto paliva násobkem hmotnosti kosmické lodi. Výhodou zde je, že produkty fúze můžou tvořit pracovní látku vytékající tryskou. Je třeba počítat s tím, že ne u všeho deuteria a hélia 3 dojde k fúzní reakci.

Ještě horší je situace v případě štěpného reaktoru. Zde je potřeba u rychlosti 0,02 c rozštěpit 22 tun čistého štěpného materiálu a pro rychlost 0,2 c pak až 2200 tun štěpného materiálu. Zde je potřeba zdůraznit, že žádný známý typ reaktoru neumožňuje rozštěpit všechna jádra paliva. V každém zůstává i značné množství uranu i transuranů vznikajících záchytem neutronu, který nezpůsobí štěpení.

Pokud bychom chtěli dosáhnout dokonce rychlosti 0,8 c, musíme kinetickou energii určit pomocí relativistické rovnice. V tomto případě by šlo o kinetickou energii stotunové lodi, která je stejná jako klidová energie necelých 67 tun hmoty. V tomto případě se kromě pohonu na antihmotu dostáváme na hmotnosti paliva o několik řádů větší, než je hmotnost lodi.

Na závěr si ještě připomeňme, že v případě popsaného letu, kdy zrychlení probíhá první polovinu letu a pak bude loď symetricky brzdit, potřebujeme dvojnásobek energie a výkony nejméně v řádu stovek GW.

Ciolkovského rovnice

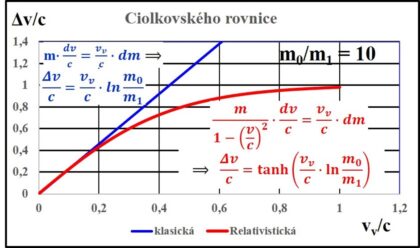
Nyní se dostáváme k Ciolkovského rovnici, která popisuje let rakety. Při urychlování totiž potřebujeme odpovídajícím způsobem měnit hybnost kosmické lodi. To se děje pomocí využití zákona akce a reakce a vytékání proudu pracovní látky tryskou. Rovnice plyne ze zákona zachování hybnosti, který můžeme v klasickém nerelativistickém případě zapsat ve formě diferenciální rovnice uvedené na grafu 3. Jde o typ diferenciální rovnice, který se vyskytuje při řešení fyzikálních problémů často a vede k exponenciální (logaritmické) funkci. Zde jsme označili jako m₀ počáteční hmotnost rakety a m₁ její koncovou hmotnost po spotřebování paliva, tedy v našem případě sledovaných 100 tun. Jako v_v je označena efektivní výtoková rychlost pracovní látky a Δv pak celková změna rychlosti, kterou raketa realizovala.

V tomto případě je poměr změny rychlosti a efektivní výtokové rychlosti roven přirozenému logaritmu poměru počáteční a konečné hmotnosti rakety. Pokud je tak požadovaná změna rychlosti menší nebo srovnatelná s efektivní výtokovou rychlostí, tak je potřebná hmotnost pracovní látky malá nebo srovnatelná s konečnou hmotností lodi. Pokud je však požadovaná změna rychlosti větší než efektivní výtoková rychlost, tak hmotnost pracovní látky velmi rychle exponenciálně roste. V grafu 3 je zobrazen příklad závislosti změny rychlosti lodě na efektivní výtokové rychlosti pro poměr počáteční a konečné hmotnosti rakety 10, tedy pro hmotnost paliva, které je devítinásobek konečné hmotnosti kosmické lodi. V našem případě hmotnosti kosmické lodi 100 tun by hmotnost paliva byla 900 tun. To je rozumná hodnota.

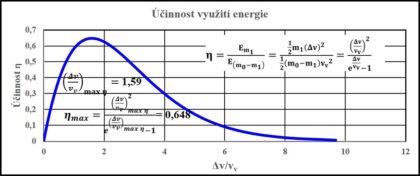
V části o potřebné kinetické energii bylo zmíněno, že se kinetická energie předává nejen urychlované lodi, ale také vyvrhované pracovní látce. Ciolkovského rovnice nám umožňuje určit závislost účinnosti využití energie na poměru dosažené změny rychlosti a efektivní výtokové rychlostí. V grafu 4 je vidět, že v optimálním případě, který je pro poměr změny rychlosti a výtokové rychlosti 1,59, je hodnota účinnosti 64,8 %. Potřebné energie, které jsme určovali v předchozí části, stačí v ideálním případě jen o něco méně než zdvojnásobit. Ovšem, pokud nebudeme v optimu, musíme mít energie mnohonásobně i řádově více. Ještě zmiňme, že poměr mezi počáteční a konečnou hmotností rakety je ve zmíněném optimálním případě 4,92.

V případě potřeby dosažení relativistických rychlostí je nutné využit speciální teorii relativity. V grafu 3 je ukázána relativistická diferenciální rovnice, kterou v tomto případě dostaneme. Z ní dostaneme uvedenou relativistickou Ciolkovského rovnici, ve které vystupuje kvůli Lorentzově transformaci tangenta hyperbolická. Pro znalejší připomenu, že v relativistickém případě se daleko lépe než s rychlostmi, pracuje s rapiditami. Stejně, jako se v případě použití logaritmů převádí násobení na sčítání, převádí se pomocí rapidity Lorentzova transformace na sčítání.  V grafu 3 je vidět, že rozdíl mezi nerelativistickou a relativistickou rovnicí se začne významněji projevovat pro rychlosti větší než 20 % rychlosti světla.

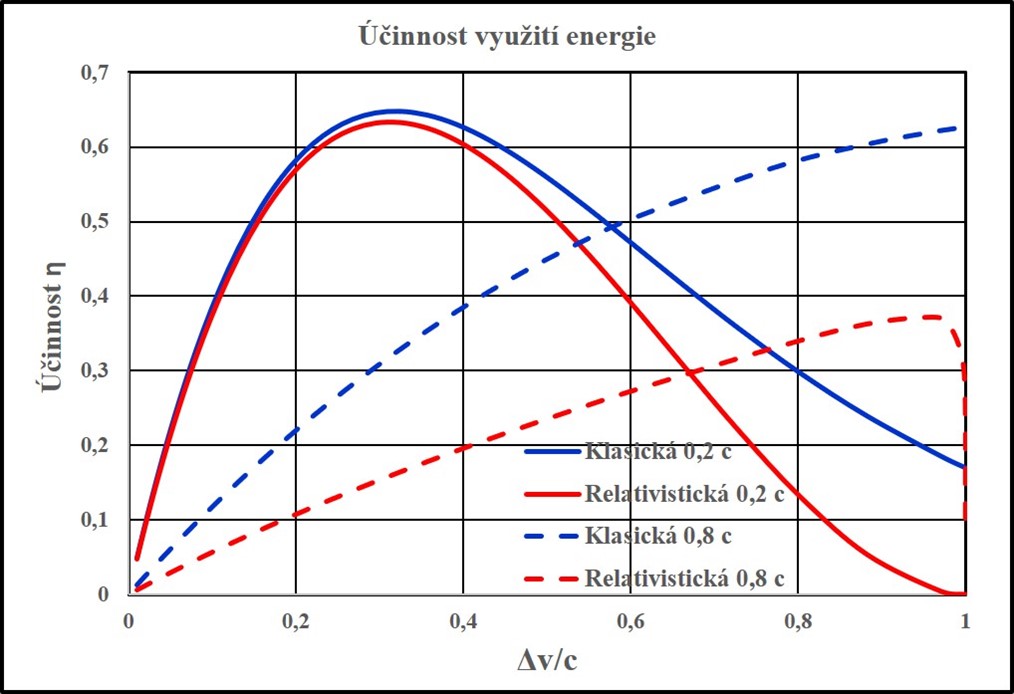
I pro účinnost využití energie lze odvodit potřebné relativistické vztahy. V grafu 5 je vidět, že pro výtokovou rychlost 0,2 c se relativistická funkce velmi dobře shoduje s nerelativistickou po změnu rychlosti rakety nepřesahující 0,2 c. Po jejím překročení se obě křivky začínají rozcházet. Maximum je opět přes 60 % a v oblasti poměru změny rychlosti lodi a výtokové rychlostí okolo 1,5. Pro výtokové rychlosti, které jsou silně relativistické, se už relativistická funkce od klasické liší i dramaticky. V grafu 5 je ukázána situace pro výtokovou rychlost 0,8 c.

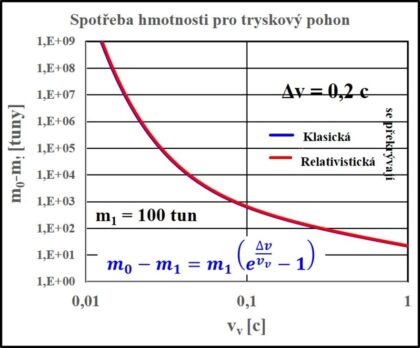
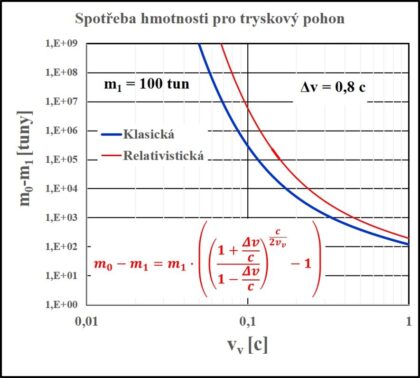
Podívejme se, kolik budeme potřebovat v našich případech s lodí o hmotnosti 100 tun pracovní látky. Její závislost na výtokové rychlosti pro námi požadované dosažení rychlosti 0,2 c je v grafu 6. Při této požadované rychlosti se výsledky relativistického a nerelativistického výpočtu shodují. Rozdíl se objevuje až v případě, kdy potřebujeme dosáhnout opravdu relativistických rychlostí, například 0,8 c, jak je vidět v grafu 7.

Připomeňme, že štěpné reaktory by mohly realizovat výtokové rychlosti maximálně okolo 40 km/s, V tomto případě by dosažení rychlosti 0,2 c potřebovalo zhruba řádově nepředstavitelných 10⁶⁵³ tun. V případě rychlosti 0,02 c je to 10⁶⁷ tun a i pro 0,002 c, což je 600 km/s, to je pořád 330 milionů tun.

Pokud bychom využily iontový motor se špičkovou hodnotou výtokové rychlosti 10 000 km/s, jsou odpovídající hodnoty pro 0,2 c celkově 40 200 tun, pro 0,02 c je 82 tun a pro 0,002 c je to už jen něco více než 6 tun. Výtokové rychlosti v řádu tisíců km/s by mohly být dostupné i v případě fúze. Anihilační pohon by mohl přiblížit výtokové rychlosti k rychlosti světla.

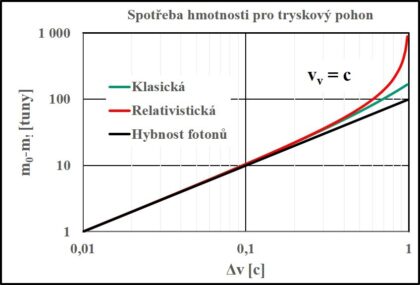
Pokud se hmota přemění na fotony, jedná se o ultrarelativistické částice, u kterých je lineární závislost mezi hybnosti a energii. Celková energie, celá je kinetická, vzniklých fotonů je dána klidovou energií anihilované hmoty a antihmoty, tedy součinem klidové hmotnosti a kvadrátem rychlosti světla. Celková hybnost fotonů, předpokládáme jejich proud v jednom směru, je součinem klidové hmotnosti původní hmoty a antihmoty a rychlosti světla. V ideálním případě je zároveň blízká hybnosti, kterou má loď po zrychlení, a potřebná celková hmotnost anihilované hmoty a antihmoty je jen o něco vyšší než hmotnost vesmírné lodi vynásobená podílem dosažené rychlosti a rychlosti světla.  K této hodnotě potřebné hmotnosti pracovní látky se blížíme při přibližování rychlosti pracovní látky k rychlosti světla. Platí to pro nerelativistické přiblížení. Pro změnu rychlosti blížící se rychlosti světla je potřebná hmotnost větší a větší. Podrobněji to ukazuje graf 8.

Jak je vidět, pro realizaci možnosti mezihvězdných letů je klíčové dosažení dostatečně velké výtokové rychlosti. Ideální je, pokud je srovnatelná s rychlostí, kterou chceme dosáhnout. V tomto případě je vysoké využití energie dosahující hodnot i přes 60 % a i hmotnost pracovní látky je srovnatelná s hmotností kosmické lodi. Pro dosažení rychlosti kosmického plavidla v řádu procent rychlosti světla to znamená, že je potřeba se dostat k hodnotám 1000 km/s až 10 000 km/s. Kromě anihilačního motoru by to mohl umožnit i ten fúzní. Ovšem ani ten zatím nemáme a není ani jasná cesta, jak k němu dospět.

Lze sice spojit štěpný reaktor s iontovým motorem, který může mít v principu výtokové rychlosti v řádu 1000 km/s. Ty však také zatím nemáme ani ve výhledu. Zde je velký problém nízké účinnosti konverze energie a dosažení odpovídajícího tahu.

Štěpné reaktory sice mezihvězdný let neumožní, mohou však přispět k realizaci podrobného studiu vnějších oblastí Sluneční soustavy. Znalosti podmínek vně heliosféry, odkud máme zatím informace pouze ze sond Voyager 1 a 2, jsou klíčové pro reálnou přípravu mezihvězdného letu. Mezihvězdná loď se v mezihvězdném prostoru bude pohybovat řadu desetiletí nebo dokonce staletí. Je třeba vědět, jak chránit elektroniku a zajistit přežití aparátů.

Závěr

Jak je vidět z předchozího rozboru, nejsou mezihvězdné lety s využitím raketové motoru realizovatelné bez osvojení využití termojaderné fúze. Kdy se to podaří, nelze odhadnout. Ještě větší výzvou je případné využití antihmoty, zde je úroveň inženýrských výzev ještě o mnoho řádů výše. V předchozím textu jsme se věnovaly pouze energetickým nárokům a požadavkům na hybnost. Doufám, že to i tak  čtenáři přiblížilo extrémní náročnost této výzvy.

Ještě bych poprosil čtenáře, který bude studovat předkládané detailněji, aby mě upozornil na případné chyby. Člověk je chybující a při práci s takto obrovskými čísly snadno udělá chybu, i řádovou. Jako se mi povedlo při přednášce pro opavskou Czech Mars society. Jak se snažím ukazovat dva příklady možných rychlostí 0,02 c a 0,2 c, tak jsem pro hodnotu 0,2 c při přednášce uváděl hodnoty potřebných hmotností (konvertované energie) pro rychlost 0,02 c.

V tomto článku se vůbec neposuzovaly extrémní technologické nároky, které jsou s vesmírnými štěpnými, fúzními i anihilačními technologiemi spojeny. Společné jsou extrémní nároky na materiály. Zásadní je pokrok v oblasti supravodivých magnetů, laserů i metod urychlování částic. Po zkušenostech v Opavě bych viděl jako velmi zajímavé realizovat několik diskuzních podvečerů o některé ze zmíněných problematik.

Dalším zásadním problémem je ochrana a odolnost před galaktickým kosmickým zářením. Této problematice se věnovalo i několik dřívějších článků (zde, zde, zde, zde a zde). Pro další informace bych doporučil cyklus článků o jaderných zdrojích pro vesmír v časopise Jaderná energie v ročnících 2022 a 2023, kde jsou na konci každého dílu i odkazy na odborné zdroje.

Psáno pro servery Osel a Kosmonautix

Nedávná přednáška o možnosti mezihvězdných letů pro Czech Mars Society v Opavě: https://www.youtube.com/watch?v=s0rZPjdmO2k

Dřívější přednáška pro stejnou organizaci o radionuklidových zdrojích a štěpných reaktorech pro vesmír: https://www.youtube.com/watch?v=rV_lWRoNODI

Přednáška z cyklu pro Czech Mars Society o ochraně před radiací ve vesmíru: https://www.youtube.com/watch?v=ohLftp-afLM