Ještě ve druhé polovině 19. století se mohlo zdát, že veškerá zásadní fyzika byla objevena a na budoucí generace odborníků čeká již jen upřesňování konstant na pátém desetinném místě. Nic však nemohlo být dále od pravdy. Nebylo totiž daleko období, kdy se začaly naplno projevovat nedostatky klasické fyziky, což vyvrcholilo velkou revolucí v prvních letech 20. století. O novém přístupu ke gravitaci, obecné teorii relativity Alberta Einsteina jsme zde už hovořili. Dnes se podíváme podrobně na druhou novou oblast, kvantovou fyziku. Při pokusu vysvětlit nesmyslné předpovědi klasické fyziky se tak trochu nechtěným ničitelem starých pořádků stal rozvážný německý fyzik a filosof Max Planck. Plný dosah Planckových kvant však dohlédl právě až Albert Einstein, jenž svým vysvětlením fotoelektrického jevu připravil půdu pro zásadní pokrok Nielse Bohra, Erwina Schrödingera, Wernera Heisenberga, Paula Diraca a dalších. Dnes si povíme více o tom, jak zdánlivě drobný nevyřešený problém ve staré fyzice přerostl všechny meze a vedl až k laserům, počítačům a kvantové komunikaci.
Ultrafialová katastrofa

Zdroj: https://upload.wikimedia.org/
Po sjednocení elektřiny a magnetismu Jamesem Clerkem Maxwellem mohl leckdo nabýt dojem, že jsou všechny zásadní fyzikální problémy vyřešeny a zbývá už jen prozkoumat pár posledních drobností a pak bude celá fyzika hotová. To byl však hluboký omyl. Právě z jedné takové otázky vznikla následně celá nová fyzika.
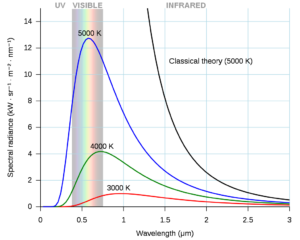
Jednalo se o problém záření absolutně černého tělesa. Černé nebo absolutně černé těleso je ideální těleso pohlcující všechno záření na veškerých vlnových délkách. Současně je však ideálním zářičem, vysílá totiž nejvíce zářivé energie ze všech myslitelných těles o stejné teplotě. Poměrně dobrým příkladem absolutně černého tělesa je třeba Slunce (o teplotě 5 800 K) nebo reliktní záření (2,7 K).
Zdroj: https://upload.wikimedia.org/
Mimochodem, možná vám pojem absolutně černé těleso připadá poněkud matoucí. Proč právě černé těleso? Postačí vědět, že fyzikové chtěli zkoumat tepelné vyzařování těles. To zní na první pohled úplně jednoduše. Jenže pokud má objekt nějakou barvu nebo odráží světlo, celá situace se tím výrazně zkomplikuje. Proto se odborníci rozhodli řešit otázku pro ideální těleso, které žádné světlo neodráží. Takové hypotetické těleso je právě naše absolutně černé těleso.
Z klasické fyziky vyplývá předpověď, že absolutně černé těleso vydává tepelné záření o nekonečném výkonu, jelikož by s klesající vlnovou délkou měla intenzita záření růst do nekonečna. Tento rozpor se objevuje nejvíce od ultrafialové oblasti směrem k vyšším energií, proto název ultrafialová katastrofa. Představte si, že si třeba zapnete troubu, abyste si ohřáli jídlo a když otevřete dvířka, záření vás usmaží k smrti. Je tedy zjevné, že někde byla chyba.
Planckův vyzařovací zákon

Zdroj: https://upload.wikimedia.org/
Odhalil ji německý fyzik Max Karl Ernst Ludwig Planck, který v roce 1900 odhadl správnou závislost intenzity záření absolutně černého tělesa na frekvenci. O rok později navíc přišel na způsob jak tento vztah matematicky odvodit. Právě za tento významný přínos světové fyzice a vědě obecně byl Planck roku 1918 oceněn Nobelovou cenou za fyziku.
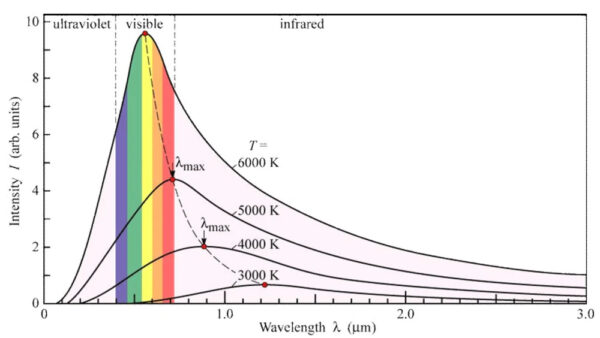
Planck se rozhodl zkusit do výpočtů zavést matematické členy, které lze interpretovat jako jakési balíčky energie (ta se tedy neemituje spojitě, jak se dříve myslelo). Tyto balíčky nazval kvanta energie, odtud kvantová teorie (mechanika, fyzika…). Pokud by energie v kvantech skutečně byla vyzařována, šlo by pozorování vysvětlit. Planckův vyzařovací zákon, jak se vztah mezi intenzitou záření absolutně černého tělesa a frekvencí nazývá, je jedním z nejdůležitějších objevů fyziky vůbec. Zajímavé navíc je, že když máme absolutně černé těleso, stačí nám k popisu distribuce jeho vyzařování jediný parametr – teplota.
Zdroj: https://static.wikia.nocookie.net/
Planckův zákon je zvláštním případem Boseho-Einsteinova statistického rozdělení pro fotony, částice světla, respektive elektromagnetické interakce. Maximum křivky je dáno Wienovým posunovacím zákonem. Čím teplejší je těleso, tím více energie vyzařuje na kratších vlnových délkách. Proto má Slunce maximum vyzařování na zcela jiné vlnové délce než například rozpálená kamna.
Einstein a fotoelektrický jev

Zdroj: https://plus.rozhlas.cz/
Pro Maxe Plancka však byla kvanta pouhou užitečnou matematickou pomůckou, nemyslel si, že reálně existují. Správný význam jim dal až o pět let později Albert Einstein, když publikoval zásadní článek vysvětlující fotoelektrický jev. V jeho zázračném roce 1905 to byl první ze čtyř publikovaných výsledků a byť je velmi těžké porovnávat jejich významnost, určitě jeden z důležitějších. Právě tento příspěvek totiž položil základy kvantové mechanice. A není tedy divu, že za něj v roce 1921 Einstein obdržel Nobelovu cenu za fyziku, nikoliv za obecnou relativitu jak si mnozí lidé myslí.
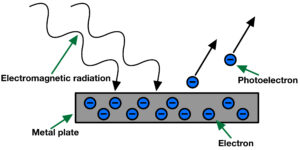
Fyzikové pozorovali, že když některé látky (především kovy) ozařujeme světlem, dochází k jejich elektrickému nabití. Elektrický náboj, který získávají je kladný, při ozáření světlem tedy dochází k uvolňování elektronů z obalů atomů a následně k jejich vyzařování z povrchu tělesa. Elektrony emitované v důsledku absorpce elektromagnetického záření nazýváme fotoelektrony.
Zdroj: https://i0.wp.com/
Fotoelektrický jev pozoroval poprvé Heinrich Hertz v roce 1887. Podle tehdy uznávaných principů klasické fyziky by měla být elektronům předána energie dopadajícího elektromagnetického záření. A protože energie elektromagnetických vln souvisí s intenzitou záření, měla by energie emitovaných elektronů záviset na intenzitě dopadajícího světla. Jenomže experimenty, které odborníci provedli překvapivě ukazovaly, že energie elektronů vyražených z látky nezávisí na intenzitě dopadajícího záření, nýbrž na jeho frekvenci. A to byl velký problém. Tehdejší vlnová teorie světla totiž nedokázala tento výsledek vysvětlit.

Zdroj: https://images.ctfassets.net/
Poradit si dokázal až v roce 1905 právě Einstein. Akceptoval Planckova kvanta jako reálná a pomocí nich rozpor vysvětlil. Uvažoval o světlu jako o proudu kvant neboli částic zvaných fotony. Energie těchto kvant závisí na jejich frekvenci podle vzorce E = hf, kde E je energie, f frekvence a h Planckova konstanta. Pokud je vlnová délka dopadajícího elektromagnetického záření dostatečně nízká, může být naopak jeho energie dostatečně vysoká k vyražení elektronu z látky.
Vysvětlením fotoelektrického jevu Einstein zasadil tvrdou ránu tehdy dominantní vlnové teorii světla. Některé experimenty sice nedokázala vysvětlit částicová teorie, avšak nyní jsme tu měli první, který nemohla naopak vysvětlit teorie vlnová. Od té doby nebyla skutečná povaha světla zcela jasná.
Atomová teorie a první modely atomu
Zdroj: https://mhcc.pressbooks.pub/
Co se naopak vědělo jistě byla skutečnost, že existují atomy obsahující záporný a kladný elektrický náboj. Od prvních kroků Rudera Boškoviče a Johna Daltona se moderní atomová teorie v průběhu století páry velmi rozvinula a povedlo se jí vysvětlit řadu chemických problémů. V roce 1897 ale anglický fyzik J. J. Thomson ukázal, že existují velmi lehké částice, později nazvané elektrony, které nesou záporný elektrický náboj. Správně také určil, že se tyto částice musí nacházet uvnitř atomů.
Zdroj: https://www.universetoday.com/
O těch se tehdy již tušilo, že opravdu existují, skutečně nezpochybnitelný důkaz předložil ale až ve svém zázračném roce 1905 Albert Einstein. Jeho článek vysvětlující Brownův pohyb, tedy náhodný pohyb mikroskopických částic v plynném nebo častěji kapalném médiu způsobují totiž právě atomy a molekuly roztoku. Smutnou skutečností je, že ani tento objev nezachránil život skvělého rakouského fyzika Ludwiga Boltzmanna, velkého zastánce a propagátora atomové teorie, který vlivem neuznání svých výsledků částí fyzikální komunity upadl do těžkých depresí a v roce 1906 spáchal sebevraždu.
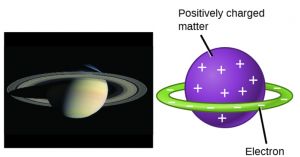
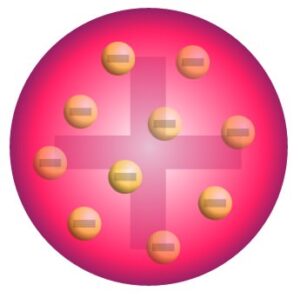
Díky práci těchto vědců se tedy již vědělo, že atomy skutečně existují (například Ernst Mach jejich reálnou existenci ale nepřijal až do své smrti v roce 1916, a to z filosofických důvodů, jelikož je nemůžeme vidět vlastníma očima). Ani v prvních letech nového století však nebylo zřejmé, jakým způsobem je náboj v atomu rozložen. Vyskytla se řada návrhů. Průkopník japonské fyziky Hantaro Nagaoka tvrdil, že atom vypadá jako Saturn. Uprostřed je masivní kladně nabitý střed kolem něhož obíhají elektrony po drahách připomínajících Saturnovy prstence. J. J. Thomson naopak domníval prosazoval myšlenku, že v atomu se vyskytují záporně nabité elektrony, které „plavou“ v kladně nabité polévce, podobně jako rozinky v pudinku.
Rutherfordův experiment
Zdroj: https://radioactivity.eu.com/
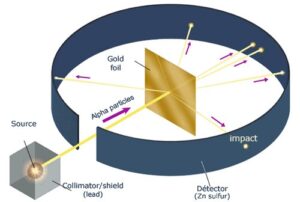
Vnitřní strukturu atomů měl prozkoumat známý experiment, v české literatuře obvykle označovaný Rutherfordův, ve světové ale spíše Geigerův-Marsdenův. Rozpor je dán tím, že přípravu a provedení pokusu vykonali německý fyzik Hans Geiger a anglicko-novozélandský fyzik Ernest Marsden, ideu ovšem navrhl jejich vedoucí na katedře fyziky univerzity v Manchesteru Ernest Rutherford, jenž na provedení experimentu odborně dohlížel a později jeho výsledky dokázal správně interpretovat.
Samotný experiment uskutečnili výzkumníci v průběhu let 1909 – 1910. Používali fólie ze zlata nebo platiny, jejichž tloušťka se pohybovala v řádu pouhých jednotek mikrometrů (miliontina metru). To odpovídá několika tisícům atomových vrstev. Tyto fólie ostřelovali alfa částicemi, což jsou jádra izotopu helia 4He a také beta částicemi, tedy elektrony. Nás dnes ale bude zajímat především to, jak dopadla měření s alfa částicemi.

Zdroj: https://upload.wikimedia.org/
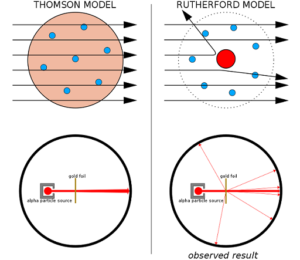
Jestliže Thomsonův model správně popisoval skutečnost, měly by alfa částice pronikat skrze fólii bez většího vychýlení, fyzikové očekávali odchýlení od původního směru letu maximálně o několik stupňů. Výsledek však odborníky šokoval. Většinu alfa částic skutečně průchod fólií neovlivnil, nebo došlo k odchýlení od původního směru letu maximálně o jeden stupeň. Avšak u malého množství částic pozorovali Geiger s Marsdenem odchýlení o mnohem větší úhel, a některé částice se dokonce od fólie odrazily a vrátily se zpět ke zdroji záření.
Rutherfordův model atomu
Zdroj: https://upload.wikimedia.org/
Novozélandskému fyzikovi bylo jasné, že bude nutné výrazně upravit stávající představu o atomech. Měřené velké odchylky některých alfa částic nebo jejich odraz ke zdroji Thomsonův model nemohl vysvětlit, záporně nabité elektrony totiž nemají dostatečný elektrický náboj nebo hmotnost, aby mohly alfa částice takto vychýlit. Rutherford si uvědomil, že se ve středu atomu musí nacházet velmi hmotný střed v němž je soustředěn kladný náboj. Prochází-li alfa částice ve směru tohoto středu nebo v jeho bezprostředním okolí, dojde k pozorovanému výraznému ovlivnění její trajektorie.
Vzhledem k tomu, že ale naprostá většina částic procházela fólií bez jakékoliv změny dráhy letu, musí být tento hmotný kladný střed ve srovnání se zbytkem atomu nesmírně malý, zatímco zbytek atomu je dosti velký a velmi málo hustý. Centru atomu říkal Rutherford nejprve těžiště, posléze ale se ale ujal název atomové jádro. Kolem ležícímu prostoru se posléze začalo říkat elektronový obal.

Zdroj: https://www.sapaviva.com/
Výsledky pokusu publikoval Rutherford v roce 1911. Definitivně jimi odmítl Thomsonův „pudinkový“ model a představil svůj vlastní model. Postuloval, že se ve středu atomu nachází malý nesmírně hustý střed s kladným nábojem, který obsahuje drtivou většinu hmotnosti atomu. Kolem něj ve velké vzdálenosti obíhají záporně nabité elektrony s velmi nízkou klidovou hmotností.
Nový Rutherfordův model znamenal velký pokrok. Představa elektronového obalu a atomového jádra, jakožto hlavní zjištění experimentu, je platná dodnes. Rutherfordův model rovněž slouží jako vzor všem dalším modernějším modelům atomu a nastartoval vývoj úplně nové disciplíny – jaderné fyziky.
Bohrův model atomu
Zdroj: https://haygot.s3.amazonaws.com/
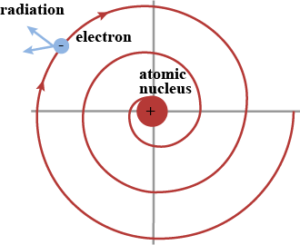
Přesto měl i Rutherfordův model atomu některé problémy. Mezi ně patřila neschopnost vysvětlit distribuci náboje elektronů a spektroskopické vlastnosti atomů. Avšak hlavní nesnáz představovala skutečnost, že by podle Rutherfordova modelu měly být atomy nestabilní. Kdyby totiž elektrony obíhaly kolem jádra jako planety kolem Slunce, docházelo by k dostřednému urychlování a podle teorie elektromagnetismu by vyzařovaly energii formou elektromagnetických vln. To by snižovalo energii elektronů, které by se postupně přibližovaly k jádru atomů, až by na něj spadly. A to velmi rychle, neboť by jim na to dle výpočtů stačilo 10-16 sekundy. Jenomže atomy existují a jsou evidentně stabilní mnohem déle, než téměř neměřitelné zlomky sekundy.

Zdroj: https://upload.wikimedia.org/
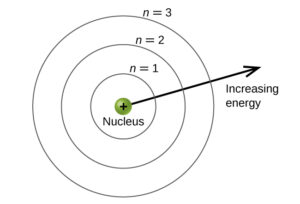
Jak z toho ven? Na to přišel dánský fyzik Niels Bohr, mimochodem úspěšný i jako fotbalový brankář. Bohr navrhl v roce 1913 vlastní model atomu. Jeho model vykazoval stabilitu a navíc dokázal vysvětlit detekované spektrální čáry vodíku. Bohrův svůj model postavil na třech klíčových principech. Podle prvního se elektrony pohybují kolem jádra atomu pouze po drahách ve tvaru kružnice na nichž nevyzařují žádné elektromagnetické záření.
Tyto trajektorie přitom nemohou být libovolné, ale pouze velmi speciální. Dovoleny jsou jen takové, pro které platí 2πmerv = nh, kde n = 1, 2, 3, 4, 5… Přičemž π je zde prostě Ludolfovo číslo známé z matematiky, me představuje hmotnost elektronu, r poloměr kruhové dráhy a v rychlost elektronu. Na pravé straně vidíme h, což je Planckova konstanta (6,62607015 x 10-34 J⋅s) a n, které představuje hlavní kvantové číslo. Třetím postulátem je potom fakt, že při přechodu z nižší na vyšší hladinu elektron pohltí právě jeden foton, naopak při přechodu z vyšší na nižší hladinu elektron právě jeden foton vyzáří.
Zdroj: https://files.mtstatic.com/
Výše zmíněné hlavní kvantové číslo lze chápat jako číslo hladiny vzestupně od nejnižší 1, 2, 3… a umožňuje nám též popsat každý možný stav elektronu v atomu. Vidíte tedy, že Bohrův model funguje na kvantovém základu. Elektrony se mohou vyskytovat pouze na určitých drahách a nabývat jen určitých energií. Poloměr r atomu vodíku stanovený výpočtem odpovídá hodnotě 53 pikometrů, zatímco hodnota určená experimentálně dosahuje necelé poloviny, 25 pikometrů.
Na první pohled by se mohlo zdát, že Bohrův model jen dobře vysvětluje naměřená data, ale sám o sobě nemá žádnou přidanou hodnotu. To by byl však hrubý omyl. Kromě své schopnosti objasnění známých spektrálních čar dokázal navíc Bohr díky svému modelu rovněž předpovědět existenci sérií spektrálních čar u atomů vodíku, které v té době nebyly známy. Ukazuje se tak síla Bohrova modelu, jehož extrapolací dokážeme objevit další zajímavé skutečnosti.
Franckův – Hertzův experiment

Zdroj: https://edu.techmania.cz/
Bohrův model odborná komunita rychle přijala za správný. Už za necelý rok, na jaře 1914, totiž němečtí fyzikové James Franck a Gustav Hertz prezentovali výsledky svých pokusů, které prováděli po dobu posledních tří let. Oba muži sledovali závislost stupně ionizace atomů na energii elektronů v parách různých prvků. Nejvíce se však proslavila a i fyzikálně nejdůležitější je varianta s parami rtuti.
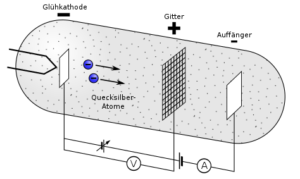
Těmito parami plnili triodu (elektronka se třemi elektrodami), respektive tetrodu (elektronka se čtyřmi elektrodami). Žhavená katoda slouží jako zdroj elektronů, které následně urychluje elektrické pole ke kladně nabité mřížce. Při cestě mezi elektrodou a mřížkou narážejí elektrony do atomů par rtuti. Rozdíl hmotnosti atomů rtuti a elektronů je značný, proto nejprve převažují pružné srážky, při kterých dochází k zachování kinetické energie elektronů, zato se ale mění směr jejich pohybu.
Zdroj: https://upload.wikimedia.org/
Při vyšším urychlení elektronů dojde k tomu, že se jejich srážky s elektrony stanou nepružnými. Tento typ srážky kinetickou energii nezachovává. Elektrony proto předají svou energii atomům, které se tak dostanou do excitovaného stavu, tedy jejich energetický stav přechází na vyšší hladinu. Elektron se naopak zpomalí a ztratí část energie, takže již nedokáže překonat brzdící napětí mezi mřížkou a anodou a k anodě se proto nedostanou.
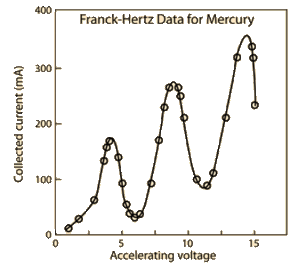
Franck a Hertz měřili závislost elektrického proudu tekoucího měřičem na napětí mezi katodou a mřížkou. Po provedení pokusu obdrželi zvláštní křivku s řadou maxim a minim. Přitom podle klasické fyziky by měli dostat monotónní rostoucí funkci. Klasická fyzika neumožňuje vysvětlit pozorovanou skutečnost. To je možné jen v případě, že přijmeme Bohrův kvantový model atomů jako správný.
Zdroj: http://hyperphysics.phy-astr.gsu.edu/
Proč? Už jsme se zmínili o nepružných srážkách, při nichž ztrácejí elektrony energii. Za běžných podmínek je většina atomů v základním stavu a právě jen s takovými atomy se elektrony srážejí. Díky Bohrovi už také víme, že energie atomů je kvantovaná a může se měnit jen skokově, nikoliv spojitě. Mezi energií základního a nejnižšího excitovaného stavu je určitý rozdíl. Proto mohou atom excitovat pouze elektrony s energií vyšší, než je tento rozdíl.
Máme-li mezi katodou a mřížkou napětí menší než určitá hodnota (rozdíl potenciálů mezi základním a excitovaným stavem atomu děleno elementárním nábojem), nemůže docházet k nepružným srážkám a ani k předávání energie atomům. Dosáhne-li napětí uvedené limitní hodnoty, k nepružným srážkám a excitacím atomů může docházet. Elektrony, jež předaly svou energii atomům pak ale nemohou překonat brzdící napětí mezi mřížkou a anodou. Proto dochází k prudkému poklesu proudu v měřícím zařízení. Tento první pokles je způsoben srážkami elektronů s atomy blízko mřížky. Obdobně se pak vyskytují další poklesy dané srážkami v jiných místech aparatury (pro dvojnásobné napětí v polovině mezi katodou a mřížkou a u mřížky, pro trojnásobné pak ve třetině, dvou třetinách a u mřížky).

Zdroj: https://orseus.imgix.net/
Odlišné prvky se v pokusu chovají rozdílně, avšak pro rtuť zjistili experimentátoři první pokles napětí na 4,9 Voltech. Rozdíl energií mezi základním a nejnižším excitovaným stavem rtuti proto očekávali 4,9 eV. A skutečně dokázali tuto domněnku potvrdit, když ve spektru pozorovali absorpční čáru s vlnovou délkou 253,6 nm, což odpovídá energii 4,9 eV. Pro zajímavost, při opakování experimentu se mnohdy užívají jiné látky než nebezpečná rtuť, kupříkladu inertní neon, pro nějž je energie potřebná k uvedení jeho atomů do prvního excitovaného stavu 18,5 eV.
Sommerfeldův model atomu

Zdroj: https://edu.techmania.cz/
Franck a Hertz tedy dokázali platnost Bohrova modelu atomu, za což získali v roce 1925 Nobelovu cenu za fyziku, zatímco sám Bohr obdržel prestižní ocenění o tři roky dříve. Tady by tedy náš příběh mohl skončit. Jenže bohužel (nebo naštěstí, záleží zda máte rádi kvantovou fyziku), není tomu tak. Dokonce i úspěšný Bohrův model měl svá omezení.
Tak především, dobře funguje pouze pro atom vodíku a pro takové ionty, které v elektronovém obalu disponují pouze jediným elektronem (He+, Li2+, Be3+…). U atomů s více elektrony nepředpovídá Bohrův model správné výsledky. Bylo tedy zřejmé, že i tento model bude nutné nahradit jiným.
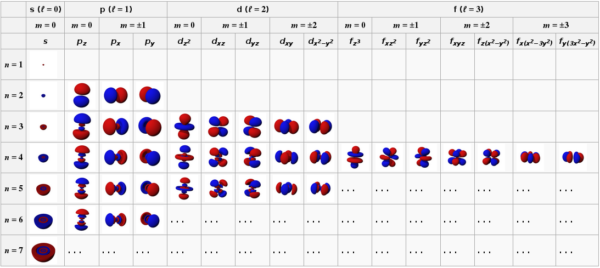
A to i přes určitá vylepšení německého fyzika Arnolda Sommerfelda, mimochodem smutného rekordmana mezi fyziky. Sommerfeld byl totiž 84 krát nominován na Nobelovu cenu, ale nikdy ji nezískal. Sommerfeld přidal k hlavnímu kvantovému číslu n i vedlejší kvantové číslo l, které určuje tvar a symetrii elektronového oblaku. Může nabývat hodnot 0, 1, 2… až do maximální meze rovné n minus jedna. Jestliže je tedy hlavní kvantové číslo atomu čtyři, pak vedlejší kvantové číslo může být maximálně tři. Používá se i alternativní značení s, p, d, f…, jež si možná pamatujete z chemie.

Zdroj: https://d10lpgp6xz60nq.cloudfront.net/
Sommerfeld navíc při oběhu elektronů kolem jádra předpovídal relativistické efekty. Elektrony se totiž pohybují (to, co vlastně znamená pohyb elektronů kolem jádra a kdy je vhodné použít jaký popis by se dal napsat dlouhý text, snad se na to dostane někdy příště) téměř rychlostí světla, přičemž blízko jádra je rychlost nejvyšší a naopak daleko od něj nejnižší. Proto se mění i hmotnost elektronu v závislosti na fázi dráhy. Ve vysvětlení rozštěpení spektrálních čar (tzv. jemné struktury) sice oproti Bohrovu modelu přináší Sommerfeld jistý pokrok, ani on však nedokáže všechna pozorování uspokojivě vysvětlit.
Přesto nešlo o žádné fiasko. Bohrův model představoval důležitý mezičlánek ve vývoji kvantové fyziky a stále je užitečnou pomůckou při snaze popsat stavbu elektronového obalu. Podobně Sommerfeldův model se v některých ohledech hodí, neboť dává přibližně správné výsledky. Jestliže je chápeme jako určité zjednodušení, nikoliv jako skutečnost, můžeme oba modely dodnes používat.
Sternův – Gerlachův experiment

Zdroj: https://www.biografiasyvidas.com/
Bohrův a Sommerfeldův model atomu se někdy označuje jako poslední úspěch staré kvantové teorie, v níž se kvantové jevy vysvětlovaly v rámci klasické fyziky a pravidla kvantování se používala dosti svévolně. Postupem času ovšem začalo být jasné, že je takový přístup neudržitelný. První náznak v experimentální fyzice přinesli němečtí fyzikové Walther Gerlach a Otto Stern.
Otto Sterna, teoretického fyzika z univerzity ve Frankfurtu nad Mohanem, napadla možnost testovat hypotézu o kvantovaném momentu hybnosti atomů stříbra v roce 1921. Protože ale spíše ovládal teorii, rozhodl se požádat o pomoc kolegu Walthera Gerlacha (nemá nic společného s Gerlachovským štítem) z téže univerzity, avšak z experimentálního oddělení. Uvedení myšlenky do praxe trvalo pouhý rok, v roce 1922 Gerlach provedl klíčovou sérii pokusů. Stern mu nemohl asistovat, přijal totiž profesuru v Rostocku a byl zaneprázdněn povinnostmi na novém pracovišti.

Zdroj: https://www.eduspb.com/
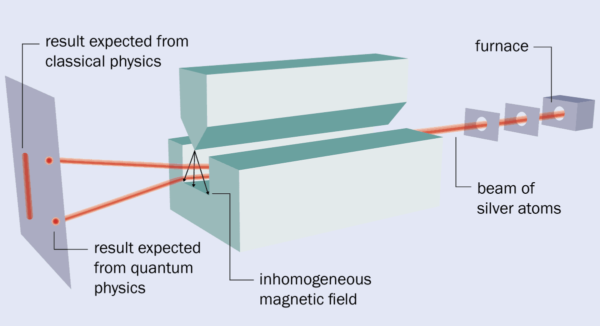
Gerlach použil jako zdroj atomů pokovenou platinovou spirálu, z níž se odpařovaly jednotlivé atomy. Jen část však prošla do kolimátoru, který je nasměroval skrze nehomogenní magnetické pole. Jím prolétly a následně byly detekovány na stínítku. Atomy použité v pokusu patřily stříbru, jež Gerlach použil jednak kvůli testování kvantové hypotézy, jednak jako vhodný elektricky neutrální pokusný subjekt. Vyloučil tím ovlivnění výsledků deformacemi drah nabitých částic v magnetickém poli.
Pokud by se částice chovaly dle zákonů klasické fyziky, mělo by vytvářet na stínítku spojitou stopu. Jak totiž částice prolétají nehomogenním magnetickým polem, dochází k ovlivňování jejich dráhy. Pokud by částice byly klasickými rotujícími dipólovými objekty, pak by rozložení vektorů jejich momentu hybnosti bylo náhodné a kontinuální.
Zdroj: https://physicsworld.com/
Jenomže to pozorováno nebylo. Výsledky ukázaly, že se na stínítku objevuje několik samostatných bodů. Z toho vyplývá, že částice mají vnitřní moment hybnosti, který je analogický s klasickým momentem hybnosti, ale může nabývat jen určitých kvantovaných hodnot. Ze získaných dat dále vyplývá, že můžeme měřit vždy pouze jednu složku tohoto vnitřního momentu hybnosti. Jestliže jej tedy chceme zjistit v ose y, nemůžeme tuto informaci najednou získat i pro osy x a z.

Zdroj: https://uwamedicalphysics.com/
Sternův – Gerlachův experiment prokázal správnost Bohrovy a Sommerfeldovy myšlenky o kvantování momentů hybnosti, současně však ukázal další neočekávané výsledky. Prokázal například, že i atomy, u nichž se očekával celkový magnetický moment roven nule, přeci jen nějaký magnetický moment mají. To je dáno elektrony ve valenční vrstvě.
V roce 1925 vyslovili George Uhlenbeck a Samuel Goudsmit tvrzení o existenci spinu u elektronů. Později se ukázalo, že spin, jakožto kvantovou vlastnost, mají všechny částice. Výsledek Sternova – Gerlachova experimentu lze proto považovat za první důkaz existence částicového spinu. V tomto případě pro částice se spinem 1/2. Spin totiž může nabývat jen poločíselných a celočíselných hodnot.

Zdroj: https://cdn02.plentymarkets.com/
Sternův – Gerlachův experiment měl obrovský vliv na fyziku, byl mnohokrát opakován, a dnes slouží jako vzor pro další pokusy kvantové fyziky. Poprvé se v něm podařilo měřit odděleně jednotlivé kvantové stavy a jde o jeden z vůbec prvních důkazů kvantování. Není proto divu, že za něj byla udělena Nobelova cena. Tu ovšem v roce 1943 získal jen Otto Stern, Walter Gerlach totiž zůstal v nacistickém Německu a dokonce se podílel na německém jaderném programu.
De Broglieho vlny

Zdroj: https://upload.wikimedia.org/
Po experimentálním triumfu Sterna a Gerlacha přišel i průlom v teorii. Zasloužil se o něj francouzský šlechtic, princ a později vévoda Louis de Broglie, který se mimochodem podílel i na založení CERNu. Jeho práce předznamenala konec klasického přístupu a začátek nové kvantové éry. Doby, kdy se zrodila moderní kvantová teorie, která změnila fyziku i běžný svět kolem nás.
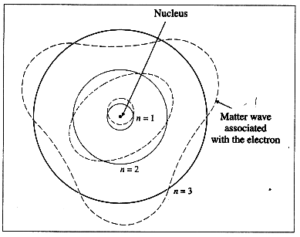
Jak jsme už zmínili, vědci věděli, že světlo vykazuje zvláštní chování, když se některé jeho vlastnosti dají vysvětlit jen částicovým modelem a jiné jen vlnovým. Inspirován debatami se svým bratrem Mauricem o rentgenovém záření a Einsteinovým přístupem ke kvantům, předložil de Broglie ve své doktorské práci v roce 1924 tvrzení o vlnové povaze elektronů. Argumentoval, že podobně jako světlo projevuje vlastnosti typické pro vlny i částice, mohou i elektrony, běžně považované za částice, vykazovat vlnové chování. Elektrony tedy mohou být kupříkladu difraktovány, stejně jako světlo nebo vlny na vodní hladině.
Zdroj: https://www.sarthaks.com/
Později se ukázalo, že vlnové vlastnosti neprojevují jen elektrony, ale všechny částice a vlastně všechny objekty kolem nás. Běžně však objekty kolem nás jako vlny nevidíme. Proč? Je to kvůli tomu, že v běžných případech je vlnová délka de Broglieho vlny daného objektu příliš malá na to, aby měla jakýkoliv praktický dopad pro běžně pozorované makroskopické jevy. Vlnovou délku λ získáme z rovnice λ = h/p, kde h je Planckova konstanta a p je hybnost. A protože je Planckova konstanta nesmírně malá, získáme pro většinu případů zanedbatelnou vlnovou délku.
Co je tedy ve skutečnosti světlo? Vlnění nebo částice? Ani jedno! Jedná se prostě o objekt mikrosvěta, který je mimo naši běžnou zkušenost. Někdy vykazuje chování vlny, jindy se projevuje jako částice, v závislosti na provedeném experimentu. Reálně však nespadá ani do jedné kategorie. To stejné platí i pro elektrony a další objekty mikrosvěta o nichž běžně uvažujeme jako o částicích. Tomuto fenoménu odborně říkáme dualita částic a vlnění nebo vlnově-částicová dualita.
Thomsonův a Davissonův-Germerův experiment

Zdroj: https://coimages.sciencemuseumgroup.org.uk/
Netrvalo příliš dlouho a de Broglieho myšlenky se rozhodlo několik vědců otestovat. Jedním z nich byl britský fyzik George Paget Thomson pracující na University of Aberdeen ve Skotsku. Mimochodem, pokud vám toto jméno připadá povědomé, máte pravdu. George P. Thomson je synem objevitele elektronů J. J. Thomsona.
Thomsonova měření spočívala ve snaze spatřit rozptyl elektronů na krystalech. Elektronové svazky posílal v pokusu skrze kovové (tvořeny obvykle zlatem, platinou nebo hliníkem) fólie, jejichž tloušťka byla jen v řádu miliontin metru. Na stínítku pozoroval difrakční obrazce, které důkladně prostudoval a dospěl k závěru, že výsledek měření je ve velmi dobrém souladu s de Broglieho hypotézou. Chyba byla jen asi plus minus pět procent, což je na tehdejší dobu krásné.

Zdroj: https://www.aps.org/
Ještě dříve, už roku 1921, začal s podobnými experimenty americký fyzik Clinton Davisson, pracovník Bellových telefonních laboratoří. Jeho experiment nebyl původně určen k testování de Broglieho hypotézy, nýbrž ke studiu rozptylu elektronů na pevné látce.
Původně pracoval Davisson s kolegou Charlesem Kunsmanem a pro experiment využíval wolfram. Roku 1923 se ale rozhodl začít používat nikl a o rok později začal spolupracovat s Lesterem Germerem, dalším Američanem z Bellových laboratoří. Jejich cílem bylo studovat povrch niklu, k čemuž chtěli využít rozptyl elektronů. Očekávali, že povrch bude pro elektrony příliš drsný a dojde k rovnoměrnému rozptylu do všech směrů. A to také pozorovali, přesně v souladu s předpovědí nizozemského fyzika Williama Bragga.
Jenže co čert nechtěl, do vakuové komory se jim dostal vzduch, což způsobilo zoxidování povrchu niklu. Rozhodli se proto kov žíhat ve vysokoteplotní peci. To sice vedlo k odstranění oxidu z povrchu, ale současně mělo za následek to, že do té doby polykrystalická struktura změnila uspořádání na několik monokrystalů s pravidelnou mřížkou. Najednou začali Davisson a Germer záhadně dostávat zcela jiné výsledky, v roce 1925 získali zvláštní difrakční obrazec.

Zdroj: https://coimages.sciencemuseumgroup.org.uk/
O rok později se Davisson zúčastnil setkání britských fyziků v Oxfordu na němž Max Born k jeho velkému překvapení ukazoval difrakční obrazce z jejich dřívějších výzkumů s Kunsmanem a argumentoval jimi ve prospěch de Broglieho hypotézy. O ní přitom neměl Davisson dosud ani tušení. Brzy se dozvěděl i to, že se jiní vědci snažili o experimentální ověření hypotézy, ale neúspěšně. Po návratu do USA s Germerem experiment vylepšili a zopakovali. Výsledky hovořily samy za sebe, získali difrakční obrazec přesně v souladu s de Broglieho hypotézou.
George Thomson a Clinton Davisson získali za potvrzení hypotézy, že částice mohou mít vlnové vlastnosti Nobelovu cenu pro rok 1937. Lester Germer jakožto Davissonův student oceněn nebyl, taková byla tehdy běžná praxe, ocenění získával jen vedoucí. Ironií osudu je skutečnost, že J. J. Thomson získal v roce 1906 Nobelovu cenu za důkaz, že elektron je částice, jeho syn byl o 31 let později oceněn za důkaz, že je elektron vlna. Inu, cesty osudu a vědeckého výzkumu jsou mnohdy nevyzpytatelné.

Zdroj: https://upload.wikimedia.org/
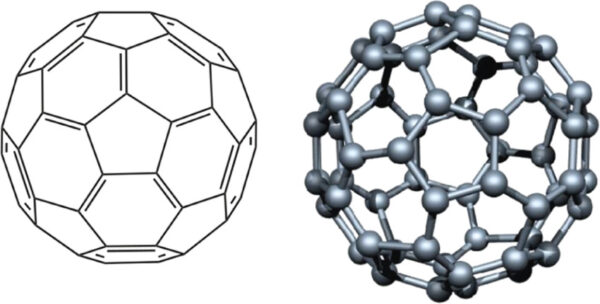
De Broglieho hypotézu později dokázali vědci i pro atomy, molekuly a dokonce makromolekuly složené ze stovek atomů. Jednou z takových molekul je kupříkladu fulleren C60 pro nějž určili výzkumníci vlnovou délku na 2,5 pm.
Dvouštěrbinový experiment
Zdroj: http://www.bottomlayer.com/
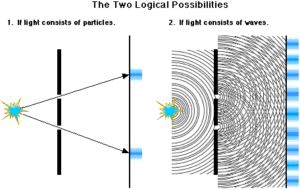
De Broglieho hypotézu dobře potvrzuje i jiný experiment, který pochází už z 19. století a vznikl původně za zcela jiným účelem. Jedná se o Youngův dvouštěrbinový experiment, jímž fyzik Thomas Young v roce 1801 prokázal, že se světlo chová jako vlnění.
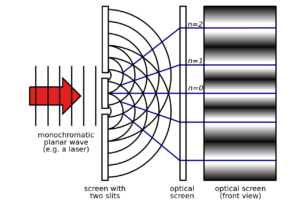
Sám Young prováděl experiment trochu jinak, nicméně dnes se ustálila podoba, kdy užijeme svazek světla, jenž necháme dopadat na stínítko. Mezi zdrojem a stínítkem ovšem umístíme clonu v níž jsou dva značně úzké rovnoběžné otvory, které leží velmi blízko k sobě. Proto dvouštěrbinový experiment. Výsledkem je, že se světelná vlna při průchodu skrze dvě štěrbiny rozdělí na dvě, které kmitají ve fázi. Na stínítku potom vidíme typický interferenční obrazec ve formě světlých a tmavých pruhů.
Zdroj: https://upload.wikimedia.org/
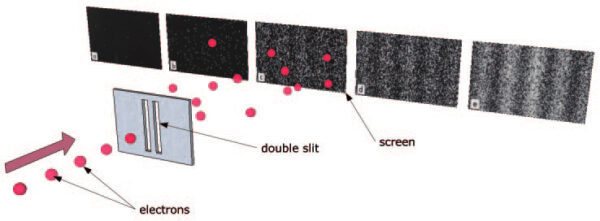
Když ovšem vstoupí do hry kvantová mechanika, věci začnou být hodně zajímavé. Místo svazku světla můžeme použít jednotlivé fotony, které budeme jeden po druhém posílat skrze štěrbiny na stínítko. Co uvidíme? Jak se bude stínítko stále více plnit tečkami po dopadu fotonů, seznáme, že i v tomto případě se nám vyskytl klasický interferenční obrazec se světlými minimy a tmavými maximy.
Vypadá to, jakoby fotony procházely oběma štěrbinami současně. Jde o skvělý příklad de Broglieho hypotézy o vlnovém chování částic. V tomto případě je částice jeden bod na stínítku zatímco vlna určitým, matematicky přesně popsatelným, způsobem koresponduje s pravděpodobností dopadu na daném místě na stínítku.
Zdroj: https://www.researchgate.net/
Představme si ale, že bychom se nespokojili s posíláním fotonů, ale chtěli bychom vždy přesně změřit jakou ze dvou štěrbin daná částice prošla. Když to však uděláme, odhalíme šokující věc. Interferenční obrazec nám zmizel. Jak je to možné?

Zdroj: https://upload.wikimedia.org/
Inu, abychom mohli změřit, kterou štěrbinou částice prochází, musíme se na ni nějak podívat. Třeba tak, že ke štěrbinám umístíme částicové detektory. No jo, jenže jak vidíme my lidé? Díky tomu, že do našich očí dopadá světlo (fotony) z okolí. A podobně je tomu i zde. Abychom zjistili dráhu částice a tím i štěrbinu, jíž prošla, je potřeba aby s ní interagovaly nějaké částice, která náš detektor zachytí.
Zatím nevidíte problém? Když se lidé dívají kolem sebe, nepředstavuje to z hlediska fyziky žádnou obtíž. Okolní objekty jsou moc velké, než aby je mohly fotony dopadající do našeho oka reálně ovlivnit. Uvědomte si ale, že u mikrosvěta je tomu jinak. Částice prolétající štěrbinami jsou podobně velké a hmotné jako částice, které s nimi interagují a díky nimž můžeme jejich trajektorii zjistit. Co je tedy v našem světě maličkost znamená ve světě kvantové fyziky významné ovlivnění procházející částice. Není tedy divu, že při pokusu o lokalizaci částice v jedné či druhé štěrbině interference zmizí.
Zde si musíme ještě ujasnit nesmírně důležitou věc. Používám tady slova jako zachytíme, vidíme atp. Tím prosím nemám na mysli to, že by byl potřeba vědomý pozorovatel. V kvantové fyzice se užívají termíny z běžného jazyka, ovšem v jiném významu. Tedy pozorovatel či pozorování zde nemusí znamenat vědomého pozorovatele a pozorování člověka či jiné inteligentní entity, ale třeba už jen zmíněnou interakci prolétající částice s jinou detekční částicí, interakci s okolím a podobně. „Pozorovatel“ zde proto může být i foton nebo elektron a pozorování pak interakce dvou částic. Pokud Vás téma vědomí v kvantové fyzice zajímá více, dovolím si vás odkázat na videa mého kolegy Radka Žemličky z kanálu Maxwellovi démoni o roli vědomí v kvantové fyzice a o tom jak se zkoumala souvislost kvantové mechaniky a parapsychologie, v nichž to rozebírá velmi podrobně.
Interferenční jev jednotlivých částic již byl pozorován u fotonů, elektronů nebo atomů. Zatím největším triumfem vědců jsou ale makromolekuly. Použit byl opět fulleren C60, ale později dokonce i molekuly s 430 (molekuly C168H94F152O8N4S4), 810 a 2000 (rok 2019) atomy. Elektrony byly také posílány přes mřížky široké jen 62 nm. Ve všech případech bylo přesvědčivě a zřetelně zaznamenáno kvantové chování. Navíc detekce jednotlivých dopadů je pravděpodobnostní, což rovněž nelze vysvětlit klasickou fyzikou.
Zdroj: https://www.researchgate.net/
S ohledem na uvedené není divu, že je de Broglieho práce dodnes uznávaná a používaná. Jak je ovšem u této části fyziky obvyklé, objevil se brzy spor o filosofický výklad problému. De Broglie tvrdil, že jsou jeho vlny spojeny s částicemi a mají přímou fyzikální interpretaci. S tím ovšem zásadně nesouhlasil jeden rakouský fyzik, který podle dostupných údajů týral nebohé kočičky.
Vlnová mechanika

Zdroj: https://www.nobelprize.org/
Erwin Schrödinger na počátku 20. let minulého století studoval strukturu atomů. Potom se ale doslechl o de Broglieho práci, silně jej ovlivnila a začal se věnovat nově se rodící kvantové fyzice. V roce 1926 publikoval v odborném časopise Annalen der Physik šest článků, v nichž popsal nový přístup k de Broglieho hypotéze i k fyzice jako celku.
Nizozemsko americký fyzik Peter Debye vyslovil na základě de Broglieho práce myšlenku, že pokud se elektron chová jako vlna, měl by splňovat nějakou vlnovou rovnici. Právě tu se Schrödinger pokusil najít. Nejprve se pokusil využít relativistický přístup, ale neuspěl. Proto se nakonec rozhodl pro řešení bez relativity a to se ukázalo jako správné. V jeho článcích z roku 1926 najdeme také novou nerelativistickou vlnovou rovnici dnes známou jako Schrödingerova.
Pomocí ní získal spektrální energie pro atom vodíku. Postupoval tak, že elektron v atomu vodíku považoval za vlnu Ψ pohybující se v potenciálové jámě vytvořené protonem. Výsledky přesně souhlasily s dosavadními poznatky o atomu vodíku. Nová rovnice sice popisovala funkci Ψ, avšak neříkala nic o její povaze. Schrödinger se nejprve pokusil interpretovat Ψ jako hustotu náboje, ale bez valného výsledku. Nicméně již roku 1926 německý fyzik Max Born správně rozpoznal Ψ jako amplitudu pravděpodobnosti.
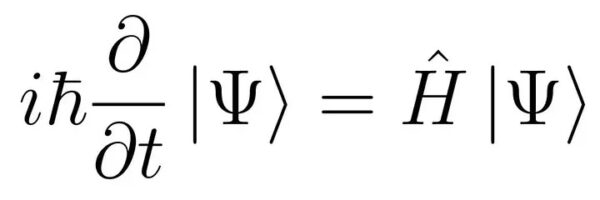
Zdroj: https://miro.medium.com/
Elektron není ve skutečnosti žádná modrá kulička běhající kolem jádra, jak vám to ukazovali ve škole, ale oblak pravděpodobnosti. Nemůžeme ani říci, kde přesně elektron v elektronovém obalu leží, lze pouze určit pravděpodobnost výskytu v daném místě. Orbitaly, jež určuje vedlejší kvantové číslo, pak určují nejpravděpodobnější oblast výskytu elektronů.

Zdroj: https://upload.wikimedia.org/
Co je vlastně ono Ψ, tedy vlnová funkce? To nám Schrödingerova rovnice neříká. Pouze dovoluje její výpočet a určení změn Ψ v čase. Význam Schrödingerovy rovnice, vlnové funkce a toho, jaký přesně mají matematické konstrukce vztah k realitě závisí na interpretaci kvantové mechaniky. Často se můžete setkat s tvrzením, že problematika interpretací kvantové mechaniky jsou jen filosofické disputace. Nicméně jsou určité interpretace, které dávají předpovědi odlišné od jiných interpretací. Experimentální naměření těchto skutečností je sice prozatím mimo naše technické možnosti, alespoň v principu však mezi některými interpretacemi rozhodnout lze (typicky GRW teorie vs. dekoherence).
Interpretací kvantové mechaniky známe celou řadu, od trochu obskurní a již zavržené von Neumannovy – Wignerovy, přes Everettovu mnohasvětovou až po klasickou Kodaňskou. Ta je čistě pravděpodobnostní, náhodná a nedeterministická, proto s ní měl Schrödinger velké potíže a ve 30. letech se definitivně odpojil od hlavního myšlenkového proudu kvantové fyziky té doby.
Maticová mechanika

Zdroj: https://i0.wp.com/
Ještě o něco málo dříve vznikla vlnová mechanika vyvinutá Pascualem Jordanem, Maxem Bornem, ale především mladičkou hvězdou německé fyziky Wernerem Heisenbergem. Také oni se snažili vylepšit Bohrovu a Sommerfeldovu práci. Na rozdíl od Schrödingera ovšem nepoužívali vlnění, ale fyzikální vlastnosti částic popsali jako soubor matic vyvíjejících se v čase. Jejich popis nahrazuje energetické dráhy atomů kvantovými skoky.
Jednalo se o první solidní formulaci moderní kvantové mechaniky. Heisenberga napadla klíčová myšlenka při odpočinku na ostrově Helgoland v Severní moři. Uvědomil si, že použití nekomutativních (komutativní = nezávisí na pořadí operací, třeba 2 + 1 = 1 + 2) operátorů by mohlo vyřešit problémy s formulací tehdejší kvantové teorie, zejména pak se správnými předpověďmi spekter atomů vodíku.

Zdroj: https://dynamic-media-cdn.tripadvisor.com/
Spíše než o zázračnou myšlenku se však jednalo o akt zoufalství. Heisenberg totiž předtím vyzkoušel všechny možné komutativní operátory, žádný postup který použil ale nevedl ke kýženým výsledkům. Proto nakonec přistoupil na možnost aplikace nekomutativních operátorů a musel připustit, že fyzika je ve svém základu nekomutativní.
Krátce na to sepsal článek, který ovšem považoval za tak odvážný, že se jej neodvážil publikovat a raději požádal o kontrolu Maxe Borna. Ten si přizval na pomoc svého kolegu Pascuala Jordana a během dvou měsíců oba muži společně článek prošli, vylepšili a připravili k vydání.
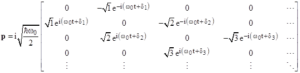
Zdroj: https://www.mathpages.com/
Maticová formulace kvantové mechaniky fyziky poněkud překvapila. Do té doby se totiž matice ve fyzice v podstatě vůbec nepoužívaly a fyzikové je brali spíše jako záležitost náležející do sféry čisté matematiky. A pokud už se matice použily, obvykle je fyzikové využili jen minimálně, protože s nimi většinou nedokázali moc dobře zacházet. V tom však byli Heisenberg, Jordan a Born výjimkou, v matematickém popisu jim navíc později pomohl americko-maďarský fyzik a matematik John von Neumann, jenž studoval u jednoho z největších matematiků historie Davida Hilberta.
Schrödingerovo a Diracovo sjednocení
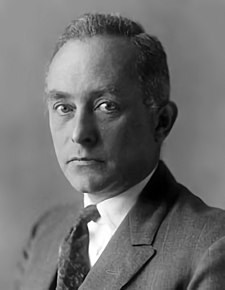
Zdroj: https://upload.wikimedia.org/
V roce 1926 jsme se dostali do dosti schizofrenní situace. Byly tu dvě formulace kvantové mechaniky. Jedna vlnová a mezi fyziky hodně oblíbená, druhá maticová a hodně matematická, jež byla alespoň zpočátku přijímána s nedůvěrou. U obou se ale zdálo, že velmi dobře fungují. Která z nich je správně?
Erwin Schrödinger brzy ukázal, že oba přístupy jsou si rovnocenné. Obě formulace kvantové mechaniky jsou tedy stejně dobré a stejně správné. Brzy přišly i úspěchy v praxi. Wolfgang Pauli předpověděl na základě nové kvantové mechaniky zcela správně spektrum vodíku a Lucy Mensing pak využila kvantovou mechaniku při práci s dvouatomovými molekulami.
Sjednocení obou přístupů definitivně dokonal britský fyzik Paul Dirac, který ve své práci z roku 1930 jednoznačně dokázal, že vlnová i maticová mechanika jsou vzájemně ekvivalentní. Obě možnosti shrnul v rámci jednotného matematického popisu. K reprezentaci fyzikálních veličin využil operátory působící na Hilbertově (vektorovém) prostoru vlnových funkcí, jež popisují stav fyzikálního systému.

Zdroj: https://library.ethz.ch/
Také v tomto případě se dočkali autoři obou formulací i následného sjednocení Nobelových cen. Schrödiger a Dirac se podělili o ocenění v roce 1933 za objev nových forem atomové teorie. Heisenberga vyznamenala komise samostatně o rok dříve. Born a Jordan, kteří k maticové formulaci výrazně přispěli byli opomenuti. Není přesně známo proč, ale pravděpodobné je, že komisi ovlivnil Jordanův vstup do NSDAP a dokonce k útočným oddílům SA. Příznačné je, že když Born získal v roce 1954 konečně Nobelovu cenu, bylo to za statistickou interpretaci vlnové funkce. Jordan se tedy prestižního ocenění nedočkal nikdy.
Heisenbergův princip
Strážník se zde ptá Heisenberga, zda ví jak rychle jel. Heisenberg na to odpovídá, že bohužel neví, zato ví přesně, kde byl.
Zdroj: https://www.eapc.net/
S Wernerem Heisenbergem souvisí ještě jeden velmi důležitý aspekt kvantové mechaniky – princip neurčitosti formulovaný v roce 1927. Tento princip (někdy též relace) nám říká, že existují dvojice propojených fyzikálních veličin, které vykazují velmi podivné chování. Čím přesněji totiž určíme hodnotu jedné z veličin, tím méně přesně můžeme určit druhou veličinu. Nejznámějším případem takových veličin je poloha a hybnost, ale princip neurčitosti platí třeba i pro čas a energii.
Konkrétně můžeme uvést vztah, že ΔxΔp ≥ ℏ/2. Δx je zde neurčitost polohy, Δp neurčitost hybnosti a ℏ je tzv. redukovaná Planckova konstanta (ℏ = h/2π). Nikdy tedy nemůžeme stanovit současně dokonale přesně hodnotu obou veličin, neboť neurčitost jejich určení musí být větší než určitá mez. Pro makroskopické objekty nehraje princip neurčitosti žádnou významnou úlohu, důležitost získává až v mikrosvětě. Velmi podobný vztah platí i pro energii a čas ΔEΔt ≥ ℏ/2.

Heisenberg zde říká, že kdykoliv měl energii, neměl čas.
Zdroj: https://i.etsystatic.com/
Mohli byste namítnout, že neschopnost určení obou veličin dostatečně přesně současně je jen věcí vyspělosti naší současné techniky. Ale tak tomu není. Princip neurčitosti platí bez ohledu na přesnost měřicích přístrojů. Jedná se o základní vlastnost kvantových systémů. Proč?
Vzpomeňte si na popis dvouštěrbinového experimentu. Když chceme měřit nějaký objekt, musíme s ním interagovat, třeba pomocí fotonů. To v běžné zkušenosti není problém, protože fotony mají ve srovnání s makroskopickými objekty zanedbatelnou hybnost a energii. Jestliže se ale chceme něco dozvědět o částicích, pak interakce s fotonem znamená ovlivnění výsledku. Takže pokud budeme chtít znát polohu částice, musíme se informace o ní dozvědět pomocí interakčních fotonů. Jenže tím částici vychylujeme a místo abychom se dozvídali více o poloze, informaci naopak rozmazáváme.
Zdroj: https://i.stack.imgur.com/
Z toho důvodu souvisí Heisenbergův princip neurčitosti velmi úzce s pravděpodobnostní povahou kvantové mechaniky, o níž jsme hovořili v předchozích podkapitolách. Tvrzení, že se částice pohybuje po dané trajektorii určitou rychlostí nemá dobrý smysl. Můžeme hovořit jen o pravděpodobnosti výskytu částice v nějakém místě.
Úvod do kvantové teorie pole

Zdroj: https://upload.wikimedia.org/
Kvantová mechanika je velmi úspěšným modelem, avšak popisuje jen stav, kdy se v průběhu času nemění počet částic a jejich druh. Odborníkům byla jasná potřeba formulace kvantové teorie pole (QFT), která by dokázala popsat chování částic, jejich vznik, zánik, změny a základní fyzikální síly.
Fyzikální teorie pracovaly s poli už od dob Newtona v 17. století. Počátkem 20. století přišly dvě velké revoluce, kvantová a relativistická. Prvním krokem bylo logicky pokusit se kvantový a relativistický přístup sjednotit. To ale nešlo úplně lehce, protože Schrödingerova rovnice je nerelativistická. Navíc sice dokáže vysvětlit situaci, kdy elektron emituje foton vlivem vnějšího elektromagnetického pole, avšak samovolnou emisi fotonu vysvětlit nedokáže.
Právě s elektromagnetickým polem, jakožto jediným tehdy známým klasickým polem, kvantoví teoretici začali. Born, Heisenberg a Jordan publikovali v roce 1926 práci v níž použili pro popis elektromagnetického pole soubor kvantových harmonických oscilátorů (fyzikální systém v němž se nějaká důležitá veličina mění v čase tak, že tyto změny popisují harmonické funkce – sinus a kosinus). Avšak jejich teorie neuměla správně předpovídat jevy ve světě kolem nás.
Zdroj: https://physicsworld.com/
O rok později zveřejnil Paul Dirac práci v níž zavedl pojem kvantová elektrodynamika (QED) pro kvantový popis elektromagnetismu. Ale co je důležitější, dokázal pomocí poruchové teorie prvního řádu vysvětlit spontánní emise. Využil při tom princip neurčitosti, podle nějž nemohou harmonické oscilátory setrvat ve stavu klidu, ale mají určitou minimální nenulovou energii. Proto oscilují vždy a to i v základním stavu. Dokonce i v dokonalém vakuu zůstává oscilující elektromagnetické pole. A právě tyto kvantové kmity elektromagnetických polí ve vakuu stimulují samovolné emise elektronů.
Jinými slovy, ve skutečnosti jsme si právě vysvětlili proč nic jako dokonalé vakuum neboli absolutní prázdnota nemůže existovat. I v tom nejlepším vakuu totiž stále zaznamenáme tzv. nulové kmity a ve skutečnosti ve vakuu probíhají poměrně bouřlivé fyzikální procesy tvorby a zániku tzv. virtuálních částic a antičástic.

Zdroj: https://www.alcf.anl.gov/
Podobně neplatí klasický středoškolský mýtus, že při teplotě 0 Kelvinů, tedy absolutní nule mají částice nulovou energii a veškerý pohyb ustane. I kdybychom 0 K mohli dosáhnout, stále by byly nulové kvantové kmity přítomny. Nic podobného není možné právě proto, že platí výše zmíněný Heisenbergův princip neurčitosti. Kdyby totiž ustal veškerý pohyb, znali bychom moment hybnosti i polohu s dokonalou přesností a to jak už víme není možné. Ale zpět ke kvantování polí.

Zdroj: https://cerncourier.com/
Pomocí poruchové teorie prvního řádu dokázal Dirac vysvětlit emise i absorpce záření. Poruchovou teorii druhého řádu využil kupříkladu k popisu rozptylu fotonů. Poruchové teorie vyššího řádu už však byly problematické, neboť se ve výpočtech začala objevovat nekonečna.
V roce 1928 poprvé Dirac formuloval slavnou relativistickou kvantovou rovnici, která dnes nese jeho jméno. Pomocí ní správně odvodil vzorec pro jemnou strukturu spektra atomu vodíku nebo vzorec pro relativistický Comptonův rozptyl. Jak jsem už zmínil, Diracova teorie je relativistická, až vám tedy bude zase někdo tvrdit, že nelze sjednotit relativitu a kvantovou fyziku, můžete odpovědět, že speciální relativitu a kvantovou mechaniku sjednotil Dirac již před téměř stoletím. Jeho rovnice vedla i na zvláštní stavy hmoty, nyní známé jako antihmota, o nichž byl jeden z minulých článků.

Zdroj: https://upload.wikimedia.org/
Ve 20. letech mezi fyziky převládal názor, že existují dvě oddělené složky hmoty, hmotné částice (elektrony, protony…) a kvantová pole (fotony…). E. Pascual Jordan, Werner K. Heisenberg, Enrico Fermi, Wolfgang E. Pauli a Eugene P. Wigner ovšem objevili, že i hmotné částice lze popsat jako excitované stavy kvantových polí.
Se zmíněnými nekonečny měli fyzikové velké potíže, špičkoví odborníci navrhli řadu metod, jak se nekonečen zbavit, uspěli ale až Julian Schwinger, Sin-Itiro Tomonaga, Richard Feynman a Freeman Dyson. První dva postupovali přísně matematicky, Feynman s Dysonem aplikovali tzv. Feynmanovy diagramy, grafickou reprezentaci výpočtů, která je sice poněkud méně rigorózní a správná, dává ale v podstatě úplně správné výsledkya to za zlomek času oproti konkurenčnímu postupu. Feynman, Schwinger a Tomonaga získali za klíčový příspěvek k rozvoji QED Nobelovu cenu pro rok 1965.

Zdroj: https://i.natgeofe.com/
Mimochodem, Freemana Dysona možná znáte kvůli jeho průniku se světem sci-fi a odvážným návrhům mezihvězdných lodí. O Feynmanovi jsme již hovořili v samostatném článku, pro nás je ale relevantní, že kromě jiného vytvořit také svou vlastní formulaci kvantové mechaniky. Jedná se o tzv. Feynmanův integrál neboli sčítání přes historie, kdy uvažujeme všechny možné trajektorie dané částice. Ta se totiž před aktem měření nachází v tzv. superpozici možných stavů z nichž kterýkoli může být alespoň v principu (pravděpodobnost se pro různé stavy dost zásadně různí) naměřen.
Moderní verze QFT se nazývá standardní model částicové fyziky a popisuje elektromagnetickou, silnou a slabou jadernou interakci, tedy všechny síly kromě gravitace. Standardní model vytvořili fyzikové v průběhu 50. – 70. let. Dodnes jde o velmi úspěšnou teorií, která byla definitivně potvrzena objevem Higgsova bosonu v roce 2012.
EPR paradox a kvantová provázanost

Zdroj: https://miro.medium.com/
Vraťme se ale do 30. let minulého století, kdy vrcholil spor mezi Einsteinem a Bohrem o povahu fyziky. Navzdory obecnému přesvědčení není pravda, že by Einstein odmítal kvantovou fyziku jako celek a ani není pravda, že jí nerozuměl. Vždyť přece pomohl kvantovou mechaniku vybudovat. Jen se mu nelíbila široce přijímaná pravděpodobnostní Kodaňská interpretace. Einstein předložil Bohrovi řadu příkladů, kdy z kvantové teorie vyplývaly paradoxní situace, Dán ale ukázal, že z těchto situací nevyplývá žádný rozpor pro předvídané výsledky měření.
Einsteinovi se například nelíbilo, že fyziky, jako je Bohr, nezajímá, jak rychle by mělo docházet ke kolapsu vlnové funkce (redukce vlnové funkce ze superpozice mnoha stavů na právě jeden vlastní stav) klidně rozprostřené celým vesmírem a rozhodně odmítal, že by ona rychlost mohla být větší než rychlost světla. Bohr však nesdílel Einsteinem kladené nároky na fyzikální teorie. Podle Bohra bylo důležité pouze to, zda teorie dává správné empirické předpovědi a ukázal, že i představa nekonečně rychlého kolapsu nezpůsobí v kvantové mechanice žádný z časových paradoxů, ke kterým vedou představy hmoty pohybující se rychleji než světlo v teorii relativity.
Zdroj: https://upload.wikimedia.org/
V roce 1935 ovšem přišlo něco speciálního. Albert Einstein se svými kolegy Borisem Podolskym (není příbuzný Jiřího Podolského) a Nathanem Rosenem publikoval myšlenkový experiment, který měl dle jejich názoru prokázat, že je kvantová mechanika neúplná a jako taková nemůže zcela přesně popsat realitu. Domnívali se, že je kvantová mechanika přiblížením nějaké jiné obecnější teorie, která ovšem není založena na pravděpodobnostním výkladu.
EPR paradox popisuje pár částic připravených v tzv. provázaném stavu. Tyto částice spolu na začátku interagují, pak se ale pohybují opačnými směry a už k žádné interakci nedochází. Pokud bychom měli částice v takovém provázaném stavu, pak bychom při změření vlastností jedné částice mohli ihned předpovědět výsledek měření u částice druhé a to bez ohledu na jejich vzájemnou vzdálenost.
Trojice autorů publikovala v roce 1935 paradox v trochu jiné podobě než jak se vykládá dnes. V podstatě šlo o snahu přesně zjistit polohu i hybnost u jedné konkrétní částice skrze provázání s částicí druhou. Tím by došlo k přesnému měření obou vlastností, aniž by vůbec došlo k fyzickému měření oné částice. EPR autoři argumentovali, že kvantová mechanika vyplývá z nějaké lokální teorie se skrytými parametry, čemuž odborně říkáme lokální realismus. Dle kritiků ovšem závisí na významu slova realita, Bohr navíc tvrdil, že poloha a hybnost se doplňují a tedy je nelze současně měřit způsobem jakým tvrdí autoři EPR a tedy Heisenbergův princip neurčitosti není porušen.

Zdroj: https://media.springernature.com/
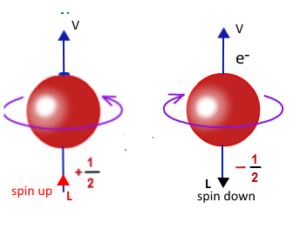
My se zde ale dnes s ohledem na názornost a na častější využití v moderních kvantových úvahách budeme dále zabývat upravenou verzí paradoxu publikovanou v roce 1951 Davidem Bohmem. Ten použil jako provázanou vlastnost spin, na němž se paradox dobře ukazuje, neboť může nabývat vždy jen dvou hodnot. Řekli jsme si, že spin u částic je vždy poločíselný nebo celočíselný. Pro konkrétní typ částice má ale spin vždy stejnou číselnou hodnotu, tak například u elektronu je to vždy 1/2.
Zdroj: https://i.stack.imgur.com/
Lišit se ovšem může něco, co bychom mohli zjednodušeně nazvat jako směr spinu. Elektron tak může mít spin orientovaný nahoru nebo dolů. Nebo, chcete-li, spin u elektronu může nabývat hodnot plus 1/2 nebo minus 1/2. To je dáno spinovým kvantovým číslem. Dva elektrony mají hlavní, vedlejší a magnetické kvantové číslo stejné, mohou se ale lišit hodnotou spinového kvantového čísla, právě ve znaménku plus nebo minus.
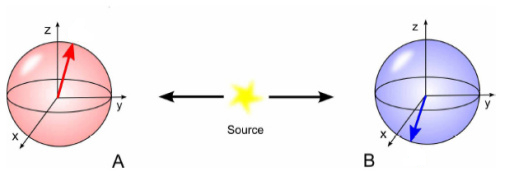
Dejme tomu, že na počátku máme elektron a pozitron (antičástice elektronu se stejnou hodnotou spinu). Částice jsou provázané, což lze chápat jako superpozici stavů, tedy laicky řečeno mohou být ve více stavech současně. Bez měření je nemožné znát spin kterékoliv z těchto provázaných částic.
Předpokládejme, že pozorovatelka Alice provede měření a získá hodnotu plus 1/2, kvantový stav se tedy zhroutil do tohoto stavu. Pokud Bob následně změří spin podlé téže osy, dostane se 100 % pravděpodobností hodnotu minus 1/2. A naopak, dostane-li Alice minus 1/2, Bob naměří plus 1/2. I pokud se rozhodnou změnit osu měření, výsledky zůstanou totožné. Tedy Bob vždy se 100 % jistotou naměří u svého pozitronu opačnou hodnotu spinu než předtím změřila u elektronu Alice.
Zdroj: https://entangledphysics.files.wordpress.com/
To (by) se ale trojici EPR nelíbilo. Zdá se, že zde došlo k přenosu informace nadsvětelnou rychlostí, což porušuje speciální teorii relativity. Tak tomu ale není. Kvantová mechanika zde skutečně porušuje princip lokality za který EPR bojovali, avšak k porušení speciální relativity nebo kauzality nedochází. Touto metodou totiž nelze nadsvětelně posílat žádné zprávy a v podstatě cíleně ani žádné informace.

Zdroj: https://www.researchgate.net/
Když se totiž Alice a Bob rozhodnou použít nějakou osu, Bob se sice dozví okamžitě spin své částice, avšak to v závislosti na měření Alice, která má ale 50 % pravděpodobnost na naměření stavu plus 1/2 a 50 % na změření stavu minus 1/2. A ať už bude jeden či druhý s osami manipulovat jakkoliv, šance 50 % se nezmění. Pro Alici je navíc nemožné ovlivnit výsledek měření, Bob zase nemůže vytvořit identické a nezávislé kopie změřených kvantových stavů a poté sledovat jejich statistické rozložení.
Bellovy nerovnosti

Zdroj: https://upload.wikimedia.org/
Většina fyziků se nadále domnívala, že je správná kvantová mechanika, jiní si ovšem mysleli, že platí nějaká verze lokální teorie se skrytými parametry. Jedná se o hypotetické vlastnosti částic, které jsou zatím nedetekovatelné, ale přesto ovlivňují a v podstatě předurčují naše měření již v okamžiku provázání, takže dojem, že dochází k náhodnému výběru naměřeného stavu je důsledkem naší neznalosti těchto proměnných, nikoli fundamentální charakteristikou přírody. Lze mezi těmito dvěma variantami rozhodnout? Ačkoliv se to může zdát neuvěřitelné, irský fyzik John S. Bell, ukázal, že to možné je.
Jeho práci dnes označujeme jako Bellův teorém, ačkoliv technicky nejde o jediné tvrzení, ale o soubor několika úzce souvisejících výsledků. Bell přišel na to, že je kvantová mechanika s lokálními teoriemi obsahujícími skryté proměnné neslučitelná a že obě možnosti dávají jiné experimentální výsledky. Bell vyšel z článku EPR a ukázal, že pro libovolnou lokální teorii se skrytými parametry platí matematická omezení korelace výsledků měření provázaných částic známá jako Bellova nerovnost. Další fyzikové pak jeho práci vylepšili a doplnili tím, že navrhli i jiné nerovnosti, takže celkově hovoříme o Bellových nerovnostech.

Zdroj: https://upload.wikimedia.org/
Tyto nerovnosti splňují lokální teorie se skrytými parametry, naopak kvantová mechanika je porušuje. Proč stále mluvím o lokálních teoriích se skrytými parametry? Je to tím, že i pokud by se prokázalo, že jsou Bellovy nerovnosti porušeny a lokální teorie se skrytými proměnnými vypadly ze hry, stále by výsledky mohla vysvětlit nelokální teorie se skrytými parametry. Jenomže v těchto nelokálních teoriích je také možná okamžitá komunikace částic bez ohledu na jejich vzdálenost, tedy něco co Einstein nazýval strašidelným působením na dálku. A proto se tato možnost většině fyziků nelíbí.
Jak ale mezi kvantovou mechanikou a lokální teorií se skrytými proměnnými rozhodnout? Podívejme se znovu na EPR paradox a provázané částice. Máme-li elektron a pozitron a měříme-li spin dejme tomu v ose y, pak při naměření spinu minus 1/2 u pozitronu víme hned, že u elektronu naměříme v téže ose spin plus 1/2. Při měření ve stejné ose budou výsledky vždy přesně opačné, tudíž jejich korelace bude minus 1, což značí dokonalou antikorelaci. Při měření v osách, které jsou vzájemně kolmé pak budou výsledky zcela náhodné, korelace proto bude nulová.
Zdroj: https://ds055uzetaobb.cloudfront.net/
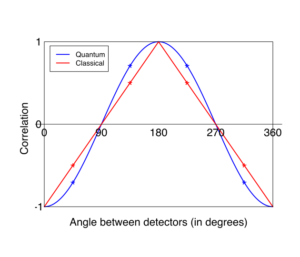
Při měření v jiných úhlech se ale výsledky obou možností liší. Lokální teorie se skrytými parametry předpovídají, že při měření v osách svírajících vzájemně úhel 45 stupňů může korelace výsledků dosáhnout hodnoty v rozmezí 0 až minus 0,5. To je dáno tím, že při shodných osách je korelace minus 1 a pro kolmé osy dosahuje korelace nulové hodnoty, pak aby pro úhel 45 stupňů byla korelace v souladu ke dvěma předchozím případům, musí být tato mezi 0 a minus 0,5.
Kvantová mechanika ale předvídá jiný výsledek. Pro osy svírající úhel 45 stupňů může korelace nabýt hodnoty až minus 0,7. To je ale v rozporu s lokální teorií se skrytými parametry. A pokud si myslíte, že si pomůžeme jiným úhlem, zklamu vás. Obdobná pravidla platí i pro jiné úhly.

Zdroj: https://sciencev2.orf.at/
Ostatně, můžeme na to přijít sami. Představme si, že máme již před měřením nějakými nám neznámými proměnnými předurčené všechny výsledky. Ať už se rozhodneme měřit v jedné, nebo druhé ose, o tom co pro každou osu naměříme je již rozhodnuto.
Víme, že v takovém případě by předurčené výsledky pro měření v horizontální ose měly mít nulovou korelaci s předurčenými výsledky pro měření ve vertikální ose. Ale co když přidáme ještě třetí osu, která bude s těmito dvěma svírat stejný úhel, tedy 45 stupňů? Ta by mohla mít s horizontální i vertikální osou korelaci maximálně 0,5, ale ne víc. Proč? Pokud bychom totiž chtěli takovou korelaci vylepšit a zvýšit ji pro horizontální osu, budeme ji snižovat pro vertikální osu a naopak. Představu, ve které by bylo to, jak měření skončí předurčeno a tyto výsledky by měly pro úhly 45 stupňů větší korelaci než 0,5 nelze tudíž vůbec vykonstruovat.
Testování Bellových nerovností

Zdroj: https://i1.rgstatic.net/
Postoj samotného Bella k celé záležitosti byl vcelku nejasný a navíc se v čase měnil. V jednu dobu stál spíše na Einsteinově straně, zastával totiž de Broglieho-Bohmovu teorii pilotní vlny, což je model operující se skrytými proměnnými (byť nelokální, což by se Einsteinovi nelíbilo). Později ale názor změnil a stal se přívržencem kvantové GRW teorie spontánního kolapsu. Sám navíc jednou řekl, že vlastně neví jaký je správný výklad kvantové mechaniky, nedomníval se, že by disponoval řešením.
Pravda je, že velká většina odborníků na kvantovou fyziku se přikláněla na stranu správnosti kvantové mechaniky. Jen nemnozí si mysleli, že by nějaká lokální teorie se skrytými parametry mohla být správná. Názory (i velmi kvalifikované) se různit mohou. Vědecký pracovník by se ale měl řídit dostupnými experimentálními daty. Co nám říkají?

Zdroj: https://www.caltech.edu/
První experiment testující Bellovy nerovnosti provedli v roce 1972 američtí fyzikové John Clauser a Stuart Freedman. Od té doby provedli přední experimentátoři z celého světa desítky experimentů. Postupně se vychytávaly chyby a odstraňovaly mezery a navíc došlo i k rozšíření metod testování.

Zdroj: https://www.nobelprize.org/
A výsledek? Dosud všechny provedené experimenty jednoznačně ukazují na správnost kvantové mechaniky. A naopak v podstatě vylučují možnost platnosti lokální teorie se skrytými proměnnými. Úplně jistě ji nemohou ovšem vyloučit nikdy, známe například hypotézu superdeterminismu, která říká, že výsledky všech experimentů jsou předem dané a to včetně předem daných os ve kterých budeme měřit a představa, že bychom se mohli rozhodnout pro měření, které není superdeterminismem předurčeno je iluzorní. Tato hypotéza je ale v principu netestovatelná a proto nepatří do oblasti fyziky.
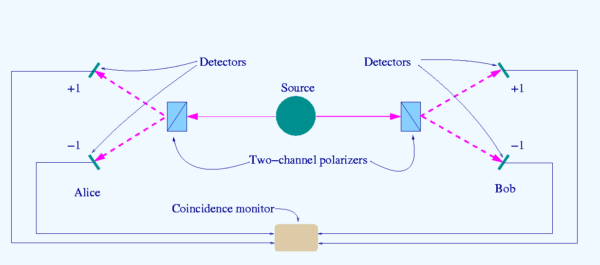
Zdroj: https://upload.wikimedia.org/
Solidní data nicméně hovoří sama za sebe. Kvantová mechanika prošla i další zkouškou a právě ona je zřejmě, alespoň dle dosavadních dat, základní teorií fyziky. Kromě Američanů Freedmana a Clausera provedli klíčová měření roku 1982 Francouzi v čele s Alainem Aspectem a v roce 1998 též rakouský tým vedený Gregorem Weihsem a Antonem Zeilingerem. Právě trojice Aspect, Clauser a Zeilinger získala za svou práci v této oblasti mnoho prestižních ocenění, naposledy dokonce i Nobelovu cenu za rok 2022. Pro Rakousko šlo o první Nobelovu cenu v oblasti fyziky za posledních 77 let.

Zdroj: https://images.deccanherald.com/
Některé další experimenty dokonce dokázaly vyloučit i specifickou třídu nelokálních teorií se skrytými parametry, z čehož vyplývá, že jakákoliv nelokální teorie konzistentní s kvantovou mechanikou musí být velmi neintuitivní. Další měření zase prokázala narušení Bellových nerovností za použití mnoha různých typů částic a existují už i pokusy, které použily současně více než dvě částice. V roce 2016 pozoroval tým v Basileji poprvé Bellovy nerovnosti v mnohočásticovém systému, když použili Boseho-Einsteinový kondenzát složený z 480 atomů.
Jen o rok později provedly týmy vedené Antonem Zeilingerem a Davidem Kaiserem experiment, kdy k testu Bellových nerovností využili světlo hvězd vzdálených 600 světelných let. Jinými slovy oblast v níž neplatí lokální teorie se skrytými proměnnými má poloměr nejméně 600 světelných let. V roce 2018 pak fyzikové použili dokonce světlo kvasarů vzdálených 7,8, respektive 12 miliard světelných let.
Kvantová teleportace

Zdroj: https://static.timesofisrael.com/
Vzhledem k výše uvedenému převládá mezi fyziky konsenzus, že žádná lokální (a některé nelokální) teorie se skrytými parametry nemohou platit a kvantová mechanika nepotřebuje žádnou úpravu či doplnění a plně funguje ve všech situacích ve své současné podobě. To umožnilo rozvoj úplně nového odvětví fyziky, kvantové teorie informace. Ta zahrnuje celou řadu fascinujících oblastí, jako jsou kvantová kryptografie či kvantové počítání. Nás ale dnes bude zajímat jen jeden podobor, a to kvantová teleportace.
Teleportace je termín, který znamená nepřímé přemisťování objektů. Jde o to, že se místo objektu samotného odesílá informace o něm, přičemž na straně přijímače se pak dle této informace vytvoří objekt totožný s původním. Takovouto teleportaci znáte z mnoha sci-fi a fantasy příběhů. Využívají ji třeba seriály Star Trek či Star Gate a objevuje se i v řadě počítačových her.

Jako v seriálu Star Trek ovšem teleportace nikdy fungovat nebude a ani nemůže.
Zdroj: https://static01.nyt.com/
Běžně uvažováná (tzv. klasická) teleportace přitom porušuje veškeré známé rovnice kontinuity. Sama kvantová mechanika má také své vlastní rovnice kontinuity a ačkoliv kvantová teleportace vyvolává dojem, že dochází k nekontinuálnímu přenosu informace, žádná z fyzikálně testovatelných rovnic kontinuity ve skutečnosti porušena není.
Klasická teleportace vychází z předpokladu, že teleportovaný objekt dokonale změříme a zjistíme o něm všechny informace, které poté klasickým kanálem odešleme k příjemci, kde dojde k rekonstrukci objektu. Jenomže kvantová teleportace takto fungovat nemůže, neboť už víme, že nemůžeme získat o nějakém objektu stoprocentně kompletní a přesnou informaci. Přesto se dá kvantová teleportace realizovat a to způsobem, který v roce 1993 navrhli Charles H. Bennett, William Wootters (oba USA), Gilles Brassard, Claud Crépeau (oba Kanada), Asher Peres (Izrael) a Richard Joszs (Austrálie).

Zdroj: https://i.ytimg.com/
Využívá se při ní tzv. qubitů. Podobně jako je základní jednotkou klasické informace bit, u kvantové informace jde o qubit. V čem je rozdíl? Klasický bit má vždy buď hodnotu 0, nebo hodnotu 1. Jenže qubit může nabývat obou hodnot současně. To je možné díky zvláštní vlastnosti zvané kvantová superpozice, kdy může být kvantový systém ve více stavech současně. Zatímco klasický bit může nést vždy maximální informaci jeden bit, qubit může nést více informace, v případě užití speciálního postupu známého jako superhusté kódování dokonce až dva bity.
K úspěšné kvantové teleportaci potřebujeme vysílač, přijímač, kvantový kanál, klasický kanál a qubit, tedy jednotku informace. Zajímavé je, že odesílatel nemusí znát přesný obsah odesílané informace. Jakým postupem můžeme teleportace docílit? Předpokládejme, že máme částici A v neznámém kvantovém stavu. Alice chce Bobovi teleportovat částici A. K tomu musí připravit další dvě částice B a C, které jsou v Bellově stavu (čtyři kvantově provázané stavy dvojice qubitů). Tento pár následně rozdělí. Částici B si Alice ponechá, zatímco částici C předá Bobovi.

Zdroj: https://light2015blogdotorg.files.wordpress.com/
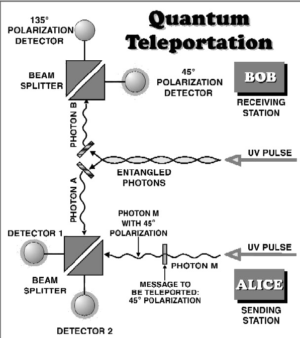
Následně Alice provede měření na částicích A a B, přičemž jako výsledek získá jeden ze čtyř možných Bellových stavů. Toto měření v tzv. provázané bázi není ani zdaleka triviální. Když se jí však podaří, promítne se původní neznámý stav částice A do stavu částice B. Řekli jsme si ale, že částice B a C jsou kvantově provázané. Ve stavu částice C vlastněné Bobem je díky tomu okamžitě zapsána informace o vstupním stavu (stavu částice A). V okamžiku měření provedeném Alicí dojde současně k přechodu kvantového stavu částice A do jiného. Stav částice A se zachová jen v provázaném páru částic B a C. Klonování stavů proto není možné, původní kvantový stav (objekt) zanikne.
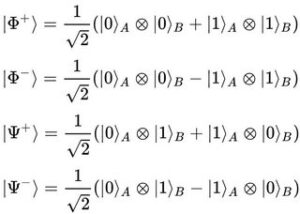
Zdroj: https://i.stack.imgur.com/
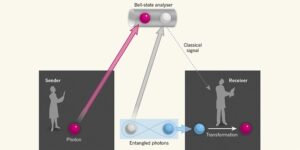
Bobovi pak už jen stačí provést transformaci částice C, čímž replikuje vstupní stav a dostává totožnou kopii původního objektu. K tomu ale potřebuje vědět, jaký výsledek naměřila Alice. Právě proto si Alice a Bob musí domluvit klasický komunikační kanál. Mohou si zavolat, napsat si email nebo napsat zprávu. Po obdržení této informace může Bob provést příslušnou transformaci a slavit úspěch. Jak ale vidíte, nelze touto cestou přenášet informace nadsvětelnou rychlostí, protože bez výsledku měření Alice je Bob bezradný, nemůže rekonstruovat původní informaci. Jenže informaci o měření si musí Alice a Bob předat klasickou, tedy podsvětelnou cestou.
Zdroj: https://media.nature.com/
Ale navíc je tu ještě jedna důležitá věc. Ani klasicky, ani kvantově předaná informace sama o sobě neříká nic o původním vstupním stavu částice A. V okamžiku provedení měření Alicí dojde ke kolapsu provázaného páru (částice B a C), čehož si ale Bob nemůže všimnout dokud mu Alice nesdělí výsledek tohoto měření. Prováděl-li by Bob měření, zjistil by, že všechny čtyři Bellovy stavy mají pro něj stejnou pravděpodobnost. Kolaps provázaného páru je sice nelokální, nenese ale žádnou informaci. A kdyby Bob věděl jen měření Alice, aniž by se realizoval zbytek procesu, také by nemohl rekonstruovat původní stav, jelikož pro stejný kvantový stav vycházejí pokaždé jiné výsledky měření.
Zdroj: https://www.researchgate.net/
Objevuje se však velký problém. Ono složité měření jímž zjišťujeme, který ze čtyř Bellových stavů se realizuje totiž neumíme provést dostatečně přesně. Dosud prováděné pokusy dokáží rozpoznat pouze dva z těchto čtyř stavů. A protože každý ze čtyř stavů má stejnou 25 % pravděpodobnost nalezení, činí úspěšnost současné teleportace 50 %. V 50 % Alice není schopná kvantový stav určit. V případě risku a provedení teleportace by se pak tato ale v polovině případů nepodařila.
Navíc když Alice provede měření a vidí, že jí nevyšel jeden ze dvou pro ni rozeznatelných stavů, nemůže už se vrátit a situaci napravit. Měření bylo provedeno a původní kvantový stav částice A přešel do jiného kvantového stavu. Jediné řešení by bylo celý experiment zahodit a připravit vše znovu, opět ale jen s 50 % šancí na úspěch u vstupního Alicina měření.

Zdroj: https://www.science.org/
Případně můžeme pracovat též s účinností 75 %, pak ale máme chybovost teleportace 25 %. U částic mikrosvěta to jistě nevadí, ale uznáte zřejmě sami, že teleportovat člověka (i kdyby to šlo, jakože nejde) s 50 % šancí na úspěch, popřípadě s chybovostí 25 % asi není to pravé. Dá se dokonce ukázat, že pomocí standardních optických prvků úspěšnost teleportace zvýšit nelze. V principu však existují postupy, jak by šlo u kvantové teleportace snížit chybovost, třeba použitím provázaného stavu více než dvou částic. Tyto možnosti jsou ale technicky podstatně náročnější, běžně se proto nevyužívají.
Navíc, pokud byste chtěli teleportovat cokoliv složitějšího než qubit, museli byste klasickým kanálem přenášet nekonečné množství informace. Jestliže byste informaci ořezali, došlo by k dalším chybám. Takže skutečná teleportace kapitána Kirka s pravděpodobností hraničící s jistotou nikdy možná nebude. Přesto ale dochází na poli kvantové teleportace k nesmírně zajímavému výzkumu.
Pozemní výzkum

Zdroj: https://simons.berkeley.edu/
Od nápadu k realizaci to v tomto případě trvalo vědcům jen čtyři roky. Už v roce 1997 provedly první praktickou demonstraci kvantové teleportace týmy rumunsko-britského fyzika Sandu Popescua a již zmiňovaného Rakušana Antona Zeilingera, které teleportovaly fotony. Tyto experimenty navíc potvrdily teoretické předpoklady o tom, jak by měla kvantová teleportace vypadat a fungovat.
V roce 2004 provedl Zeilinger se svým týmem úspěšnou kvantovou teleportaci na vzdálenost 600 metrů pod řekou Dunaj ve Vídni. Využili k tomu veřejnou kanalizaci do níž natáhli 800 metrů dlouhý optický kabel. Experiment navíc ovlivnilo vystavení kabelu změnám teplot, vlhkosti a dalším vlivům prostředí, přesto vše fungovalo bezvadně a měření splnila očekávání. V témže roce provedl tým amerického fyzika Davida Winelanda první teleportaci atomů.

Zdroj: https://freight.cargo.site/
Čínští odborníci z národní fyzikální laboratoře ve městě Che-fej dvakrát překonali nejvyšší vzdálenost úspěšné teleportace. Nejprve provedli kvantovou teleportaci na 16 kilometrů, poté dokonce na 97 kilometrů, čímž vlastní předchozí vylepšili více než šestkrát.

Zdroj: https://www.esa.int/
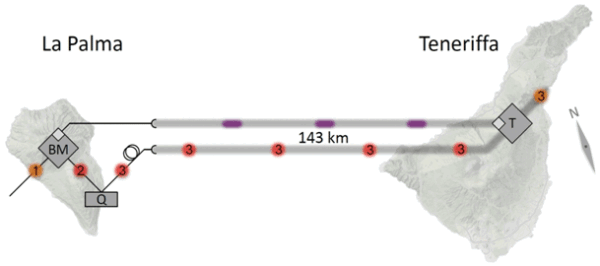
V roce 2012 si ale prvenství vzal zpět tým Antona Zeilingera, který uskutečnil kvantovou teleportaci na 143 kilometrů. Došlo k tomu na Kanárských ostrovech, kdy byly teleportovány kvantové stavy mezi ostrovy La Palma a Tenerife. Výzkumníci přitom užili zařízení náležející fyzikálnímu pracovišti Instituto de Astrofísica de Canarias. Signál posílali vzduchem, přičemž vlivem změn teploty a silného větru docházelo ke kolísání kvality přenosu, přesto opět zvládli svůj úkol na jedničku.
Americko-japonská skupina v roce 2015 zdárně vyzkoušela kvantovou teleportaci skrze optické vlákno na 102 kilometrů pomocí supravodivých nanodrátových detektorů. Pro materiálové systémy drží rekord skupina z německého institutu Maxe Plancka v Garchingu.
Zdroj: https://www.mpq.mpg.de/
V květnu 2014 bylo oznámeno zásadní zlepšení spolehlivosti kvantové teleportace, dřívější metody vykazovaly značnou chybovost. O rok později si připsali další velký úspěch čínští vědci z laboratoře v Che-fej vedení Jian-Wei Panem, kteří poprvé teleportovali více stupňů volnosti kvantové částice. Konkrétně teleportovali informace ze souboru atomů rubidia do jiného souboru atomů téhož prvku na vzdálenost 150 metrů. Stejný tým uskutečnil roku 2016 kvantovou teleportaci mezi dvěma nezávislými zdroji na vzdálenost 6,5 km. A téhož roku se podařilo kanadským fyzikům z univerzity v Calgary teleportovat kvantové stavy přes městskou optickou síť na vzdálenost 6,2 km.
Čínská družice QUESS

Zdroj: https://csis-website-prod.s3.amazonaws.com/
První pokus s kvantovou komunikací v kosmickém prostoru má na svědomí Čína. 16. září 2016 vynesla raketa CZ-2D družici Quantum Experiments at Space Scale (QUESS) určenou k testování kvantové teleportace mezi oběžnou dráhou a povrchem země. Družici se někdy přezdívá též Mozi nebo Micius podle starověkého čínského filosofa. Na projektu se kromě Číny podílejí i Rakušané, konkrétně Rakouská akademie věd a Vídeňská univerzita.

Zdroj: https://global.chinadaily.com.cn/
QUESS má hmotnost 631 kilogramů a obíhá na dráze s perigeem ve výšce 488 kilometrů a apogeem ve výšce 584 kilometrů. Sklon vůči rovníku je 97,4 stupně. Mise vyšla na 100 milionů amerických dolarů. Družice slouží jakožto technologický demonstrátor, v budoucnu by na ni mělo ovšem navázat velké množství dalších družic snad až celosvětová síť někdy po roce 2030.
Říkali jsme si, že je kvantová teleportace prakticky nevyužitelná, QUESS měl ovšem testovat též kvantovou kryptografii. Šifrování pomocí kvantové mechaniky využívá kvantové provázání a je absolutně bezpečné neboť umožňuje se stoprocentní účinností zjistit, zda nějaký špion komunikaci náhodou neodposlouchává. Pokud ano, dojde k narušení provázaného stavu a my o tom ihned víme.

Zdroj: https://www.eoportal.org/
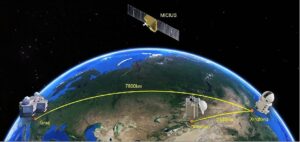
Na palubě má QUESS přístroj, který připravuje kvantově provázané stavy dvojic fotonů. Jeden z nich vždy zůstává na družici, zatímco druhý je přenesen na zem. To se využívá k celé řadě experimentů. Podařilo se například distribuovat kvantový klíč potřebný pro kvantovou kryptografii mezi družicí, astronomickou observatoří Sin-ťiang ležící nedaleko ujgurského hlavního města Urumči a observatoří nacházející se poblíž Pekingu.
Povedlo se též otestovat Bellovy nerovnosti na vzdálenost 1200 kilometrů, což je výrazně více, než co dovolily všechny dosavadní pokusy, s výjimkou astronomických. Co se týče kvantové teleportace, ta se také úspěšně podařila a to mezi družicí a observatoří Ali ležící na západě Tibetu. To je pochopitelně poměrně náročné, takže družice musela být v okamžiku teleportace ze základny Ali přímo viditelná.
Zdroj: https://www.eoportal.org/
Pomocí družice QUESS se rovněž podařilo realizovat první videohovor zabezpečený pomocí kvantové kryptografie. Uskutečnil se v roce 2016 mezi čínskými odborníky v Pekingu a Rakušany ve Vídni, které nezastupoval nikdo jiný než Anton Zeilinger. Původně určené životnosti dvou let dosáhla QUESS v září 2018, ale fungovala dále bezvadně, proto došlo k prodloužení mise. A roku 2021 se podařila kvantová teleportace na vzdálenost 1200 km, čímž čínští experti výrazně překonali vlastní rekord z roku 2017, kdy vědci uskutečnili teleportaci na vzdálenost 500 km mezi družicí a městy Delingha a Lijiang. S ohledem na to, že QUESS zatím stále funguje, zřejmě se ještě dalších zajímavých výsledků dočkáme.
Americká snaha

Zdroj: https://upload.wikimedia.org/
Čína ovšem nezůstala se svým záměrem kvantové komunikace z kosmického prostoru samotná. Své chtěli k této oblasti říci i Američané. Známá organizace DARPA rovněž vyvíjela vlastní družici určenou ke kvantové komunikaci. Měla se jmenoval Quiness a její cíle měly být podobné jako u QUESS. Tedy především otestovat možnosti kvantové komunikace. Řekli jsme si totiž, že jsou kvantové stavy extrémně citlivé na vliv okolního prostředí. Pro dosažení spolehlivé kvantové komunikace je proto nutné nejprve provést řadu precizních testů.
Quiness měla testovat tradiční stavy se dvěma kvantově provázanými částicemi, ale i stavy u nichž je kvantově provázáno více částic. A tyto stavy měla přenášet na velkou vzdálenost. Odborníci chtěli též otestovat nové kvantové protokoly a nové typy kódování, jež by mohly umožnit přenos většího množství dat. Hlavní cíl mise ale představoval test přenosu informací kvantovou cestou na vzdálenost 1 000 – 10 000 km rychlostí 1 – 10 Gb za sekundu. Zatímco je totiž kvantová komunikace velmi bezpečná, dosud zrovna nevyniká rychlostí. U klasické komunikace řešíme přesně opačný problém.
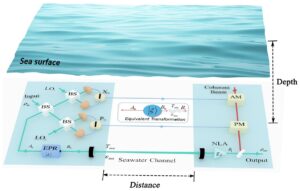
Zdroj: https://www.mdpi.com/
Bez zajímavosti není ani skutečnost, že se DARPA chtěla pokusila otestovat kvantovou komunikaci do té doby nemyslitelnými způsoby. Plánovala například vysílat z družice pod vodní hladinu, nebo do přijímače přes špinavý vzduch. Obě tato prostředí prudce snižují účinnost kvantové komunikace nebo ji dokonce úplně ruší. Úspěch mise by velmi pomohl ve snaze o vytvoření nějaké formy větší kvantové sítě, v níž by šlo bezpečně sdílet informace mezi družicemi a mnoha místy na zemském povrchu.
Vše bylo na dobré cestě, v roce 2012 se počítalo se startem do pěti let. Hlavní komunikační stanice se měly nacházet na Havajských ostrovech, konkrétně na ostrovech Havaj a Maui a i na tomto projektu se měl podílet rakouský fyzik Anton Zeilinger, hlavní hvězda oblasti kvantové komunikace. Jenomže, jak už to často chodí, přišly škrty v rozpočtu. Americké experty vývoj velmi zklamal, fyzik Ivan Deutsch z University of New Mexico označil rozhodnutí za krátkozraké. Ale stalo se a proto si většinu úspěchů plánovaných pro družici Quiness připsali Číňané s projektem QUESS.
Evropské plány
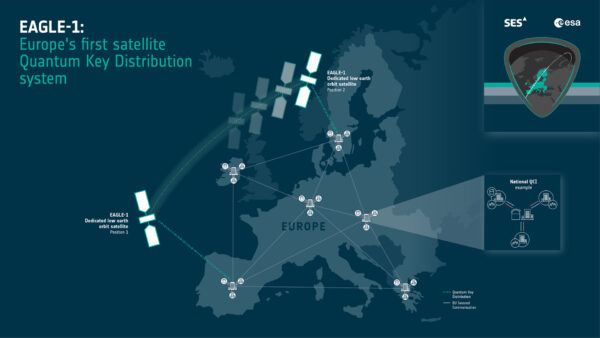
Rovněž i Evropa touží po vlastní družici určené ke kvantové komunikaci. Současný projekt s názvem Eagle-1 vzniká ve spolupráci Evropské kosmické agentury, Evropské komise a evropských firem zaměřených na oblast kosmického průmyslu. Start v tuto chvíli plánuje ESA na rok 2024 a plánovaná životnost by měla dosáhnout tří roků.
Zdroj: https://www.esa.int/
Cíle Eagle-1 budou velmi podobné úkolům, jež plní čínský QUESS i zamýšlenému programu družice Quiness. Projekt by tedy měl připravit cestu k bezpečné evropské síti postavené na principu kvantové komunikace, testovat kvantovou distribuci klíčů mezi oběžnou dráhou a povrchem Země a ve stejném režimu také provádět kvantovou teleportaci.

Zdroj: https://www.esa.int/
Družici o plánované hmotnosti asi 300 kilogramů postaví italská firma Sitael, o provoz se bude starat lucemburská společnost SES, zařízení pro vytváření kvantově provázaných stavů dodá německá firma Tesat Spacecom a pozemní stanice připraví Němci a Nizozemci. Kromě toho se na projektu podílejí i další členské státy ESA, zejména , Belgie, Rakousko, Švýcarsko a k naší velké radosti rovněž i Česko.

Zdroj: https://www.iqoqi-vienna.at/
O vynesení na heliosynchronní oběžnou dráhu ve výšce 500 km se postará společnost Arianespace, která družici vypustí na palubě rakety Vega-C. Díky tomu proběhne každý den několik průletů nad evropskými sledovacími stanicemi, což pro testování plně postačí. Celý projekt by měl přijít asi na 130 milionů euro.
Vložené prostředky se ale vrátí, neboť Eagle-1 představuje klíčový krok pro plánovanou evropskou družicovou síť založenou na principu kvantové komunikace European Quantum Communication Initiative (EeroQCI), projektu podporovaného Evropskou unií a Evropskou komisí, která také celý program finančně podporuje. Soukromé společnosti se naopak účastní v naději na komercionalizaci a rády by do budoucna globální komerční službu založenou na kvantové komunikaci.

Zdroj: https://media2.spaceref.com/
Existují ale i další projekty na kvantově komunikační družice. ESA spolupracuje s britskou společností Arqit, která by rádi vypustila vlastní družici věnující se této oblasti. Na projektu se podílejí i některé nečlenské státy EU, proto zde není podpora EU. No a společnost SpeQtral původem ze Singapuru připravuje družici SpeQtral-1, která by se měla do kosmu dostat v roce 2024, přičemž o pozemní komunikační zařízení se postará známá společnost Thales Alenia Space.
Závěr
Ne nadarmo se říká, že 20. století bylo stoletím jaderným, ale 21. století bude stoletím kvantovým. V průběhu uplynulých desítek let jsme pomalu budovali kvantovou fyziku a poznávali její složitosti a zvláštnosti. A ovšem, že jsme kvantovou mechaniku využívali, ostatně technická zařízení kolem nás jsou toho důkazem. Ale teprve nyní začínáme objevovat možnosti aplikace téměř všech kvantových zákonů a principů, dokonce i těch na první pohled zcela nevyužitelných. Současný vývoj kolem kvantové komunikace ukazuje, že se ve velmi brzké době dočkáme dalších mimořádně zajímavých výsledků.
Poznámky autora
- Za kontrolu textu a cenné připomínky, návrhy a vylepšení děkuji svému kamarádovi a kolegovi fyzikovi Radku Žemličkovi, který je autorem YouTube kanálu Maxwellovi démoni.
- Žádný delší text už ode mě pravděpodobně na tomto webu nevyjde. Naopak nyní se v řadě dalších článků mohu (a také budu) na tento text odkazovat.
- Tímto plním slib Dušanu Majerovi, že o problematice kvantových pokusů na oběžné dráze napíšu. Současně se Dušanovi upřímně omlouvám, že to od jeho žádosti trvalo tři roky.
Použité a doporučené zdroje
- Institute for Quantum Optics and Quantum Information Vienna (pracoviště Antone Zeilingera): https://www.iqoqi-vienna.at/
- John F. Clauser: https://www.johnclauser.com/
- Université Paris-Saclay (pracoviště Alaina Aspecta): https://www.universite-paris-saclay.fr/
Doporučená literatura
- Tony Hey, Patrick Walters – „The New Quantum Universe“ – česky jako „Nový kvantový vesmír“ (Argo a Dokořán, 2005)
- Chad Orzel – „How to Teach Physics to Your Dog“ – česky jako „Jak naučit svého psa fyziku“ (Argo a Dokořán, 2011)
- Brian Cox, Jeff Forshaw – „ The Quantum Universe: Everything That Can Happen Does Happen“ – česky jako „Kvantový vesmír“ (Argo a Dokořán, 2014)
- Robert Crease, Alfred Goldhaber – „ The Quantum Moment“ – česky jako „Kvantový moment“ (Argo a Dokořán, 2018)
- Robert Gilmore – „Alice in Quantumland“ – česky jako „Alenka v říši kvant“ (Paseka, 2007)
- Richard Feynman – „QED: The Strange Theory of Light and Matter“ – česky jako „Neobyčejná teorie světla a látky“ (Aurora, 2001)
- Thibault Damour – „Le Mystère du monde quantique“ – česky jako „Záhady kvantového světa“ (Argo, 2018)
- Marcus Chown – „Quantum Theory Cannot Hurt You“ – česky jako „Kvantová teorie nikoho nezabije“ (Kniha Zlín, 2010)
- Carlo Rovelli – „Helgoland“ – česky jako „Helgoland“ (Argo a Dokořán, 2023)
Zdroje obrázků
- https://upload.wikimedia.org/wikipedia/commons/3/32/Double-slit_experiment_results_Tanamura_4.jpg
- https://upload.wikimedia.org/wikipedia/commons/thumb/2/25/The_Sun_by_the_Atmospheric_Imaging_Assembly_of_NASA%27s_Solar_Dynamics_Observatory_-_20100819-02.jpg/628px-The_Sun_by_the_Atmospheric_Imaging_Assembly_of_NASA%27s_Solar_Dynamics_Observatory_-_20100819-02.jpg
- https://upload.wikimedia.org/wikipedia/commons/1/19/Black_body.svg
- https://upload.wikimedia.org/wikipedia/commons/c/c7/Max_Planck_1933.jpg
- https://plus.rozhlas.cz/sites/default/files/images/02276913.jpeg
- https://i0.wp.com/thescienceandmathszone.com/wp-content/uploads/2021/03/IMG_1042-2.jpg?fit=2402%2C1205&ssl=1
- https://images.ctfassets.net/4yflszkpcwkt/4WpadsRFlah8pnsRPHXSsr/82d2173b8e8d2aae6706470fc5c1a1a1/gggg1.png
- https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-20-at-2.29.09-PM-300×157.png
- https://www.universetoday.com/wp-content/uploads/2009/08/plum-pudding-model.jpg
- https://radioactivity.eu.com/static/7a80ee3339ead92399495c8a6a08c6ed/d1f95/ExpRutherford_En.jpg
- https://upload.wikimedia.org/wikipedia/en/2/24/Geiger-Marsden_apparatus_photo.jpg
- https://upload.wikimedia.org/wikipedia/commons/thumb/f/f9/Geiger-Marsden_experiment_expectation_and_result.svg/800px-Geiger-Marsden_experiment_expectation_and_result.svg.png
- https://www.sapaviva.com/wp-content/uploads/2017/06/22S.-Ernest-Rutherford-1871-1937-656×656.jpg
- https://haygot.s3.amazonaws.com/questions/1766649_1842952_ans_6354fb7a1682490ebeb4a90d2efe5289.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/5/5e/Niels_Bohr_Date_Unverified_LOC.jpg/499px-Niels_Bohr_Date_Unverified_LOC.jpg
- https://files.mtstatic.com/site_4334/71006/0?Expires=1697685235&Signature=K-bRWF7MZZYabDDsC8XCMEBeXUTPOXsYDhdeYMZj8KV-8v4InwNEt84j-4R3QZMB2eH9BUVJcCa2i8r3V3UugLClEnOvSjwfAL6~QAUFnsUyU3pi~miqIgNPK1GUaF4bDkg-ra4nHnd3PJVYd5zK3UO2K6QtncWI8Je~WOC-2mQ_&Key-Pair-Id=APKAJ5Y6AV4GI7A555NA
- https://edu.techmania.cz/sites/default/files/vedci/insert/franck_portret.jpg
- https://upload.wikimedia.org/wikipedia/commons/thumb/0/0a/Franck-hertz-experiment-vacuum-tube_DE.svg/474px-Franck-hertz-experiment-vacuum-tube_DE.svg.png
- http://hyperphysics.phy-astr.gsu.edu/hbase/imgmdl/FHzd.gif
- https://orseus.imgix.net/resources/images/original/wow_articles/11192/9492.jpg
- https://edu.techmania.cz/sites/default/files/vedci/insert/sommerfeld_portret.gif
- https://d10lpgp6xz60nq.cloudfront.net/physics_images/BRS_QB_PHY_SCI_X_C06_E09_029_S01.png
- https://www.biografiasyvidas.com/biografia/s/fotos/stern_otto.jpg
- https://www.eduspb.com/public/img/biography/g/gerlach1.jpg
- https://physicsworld.com/wp-content/uploads/2022/10/Johnston-diagram.png
- https://uwamedicalphysics.com/wp-content/uploads/2014/11/Pittsburgh-stern-gerlach.jpeg
- https://cdn02.plentymarkets.com/jd5w7us67fek/item/images/9233/full/p2511101i-1692069110.png
- https://upload.wikimedia.org/wikipedia/commons/d/d2/Broglie_Big.jpg
- https://www.sarthaks.com/?qa=blob&qa_blobid=11435671934753626961
- https://coimages.sciencemuseumgroup.org.uk/images/55/21/medium_1948_0024.jpg
- https://www.aps.org/programs/honors/history/historicsites/images/davisson_germer.webp
- https://coimages.sciencemuseumgroup.org.uk/images/31/555/medium_1948_0190_0001.jpg
- https://upload.wikimedia.org/wikipedia/commons/e/e9/Bell_Labs_APS_plaque_west_side_of_Westbeth_door_jeh_edited.jpg
- http://www.bottomlayer.com/bottom/reality/images/lightslitpossible.GIF
- https://upload.wikimedia.org/wikipedia/commons/thumb/8/8b/Two-Slit_Experiment_Light.svg/1280px-Two-Slit_Experiment_Light.svg.png
- https://www.researchgate.net/profile/Mehul-Malik/publication/262937062/figure/fig2/AS:667093229895684@1536058828277/A-schematic-of-Youngs-double-slit-experiment-performed-with-electrons-Plates-a-e.ppm
- https://upload.wikimedia.org/wikipedia/commons/7/7e/Double-slit_experiment_results_Tanamura_2.jpg
- https://www.researchgate.net/publication/338650435/figure/fig4/AS:11431281120123196@1676379441728/Schematic-representation-2D-and-3D-of-the-fullerene-structure-C60.jpg
- https://www.nobelprize.org/images/schrodinger-12988-portrait-medium.jpg
- https://miro.medium.com/v2/resize:fit:720/format:webp/0*iZPs3b28ttOft7Xf.jpg
- https://upload.wikimedia.org/wikipedia/commons/b/bd/Grave_Schroedinger_%28detail%29.png
- https://i0.wp.com/www.themarginalian.org/wp-content/uploads/2018/02/heisenberg_engagement.jpg
- https://dynamic-media-cdn.tripadvisor.com/media/photo-o/23/2a/87/ef/gedenkstein-fur-werner.jpg?w=1200&h=1200&s=1
- https://www.mathpages.com/home/kmath698/kmath698_files/image058.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/f/f7/Max_Born.jpg/225px-Max_Born.jpg
- https://library.ethz.ch/en/locations-and-media/platforms/virtual-exhibitions/wolfgang-pauli-and-modern-physics/_jcr_content/par/fullwidthimage/image.imageformat.930.1550178976.jpg
- https://www.eapc.net/wp-content/uploads/2017/04/speeding-ticket-400×286.jpg
- https://i.etsystatic.com/24531581/r/il/6bbb3e/2492114122/il_fullxfull.2492114122_28d1.jpg
- https://i.stack.imgur.com/EHl1o.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/a/a6/Pascual_Jordan_1920s.jpg/225px-Pascual_Jordan_1920s.jpg
- https://physicsworld.com/wp-content/uploads/1998/02/pw1102091.gif
- https://www.alcf.anl.gov/sites/default/files/styles/965×543/public/Lattice%20QCD_Sugar_0.jpg?itok=AxWR7sbc
- https://cerncourier.com/wp-content/uploads/2002/08/cerndirac3_9-02.jpg
- https://upload.wikimedia.org/wikipedia/commons/3/3c/Schwinger.jpg
- https://i.natgeofe.com/n/64ef565d-f90e-43fe-91f9-ce94001385bd/01_freeman_h_15070220_4x3.jpg
- https://miro.medium.com/v2/resize:fit:505/1*hxstCLvC7Eyv9GchZC9spA.jpeg
- https://upload.wikimedia.org/wikipedia/en/6/65/Ebohr4.gif
- https://media.springernature.com/full/springer-static/image/art%3A10.1038%2Fnphys3328/MediaObjects/41567_2015_Article_BFnphys3328_Figa_HTML.jpg
- https://i.stack.imgur.com/5isZj.png
- https://entangledphysics.files.wordpress.com/2015/05/bohm.png
- https://www.researchgate.net/profile/Olivier-Rousselle-2/publication/343654814/figure/fig29/AS:926573230292993@1597923681365/Einstein-Podolsky-et-Rosen.jpg
- https://upload.wikimedia.org/wikipedia/commons/c/c3/John_bell_2.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/0/02/Doppelspalt.svg/800px-Doppelspalt.svg.png
- https://ds055uzetaobb.cloudfront.net/brioche/uploads/ZLi7tLNa8E-bell.png?width=1200
- https://sciencev2.orf.at/v2static/storyimages/site/science/20140727/IMG_0145.jpg
- https://i1.rgstatic.net/ii/profile.image/1129626390798336-1646335327133_Q512/John-Clauser.jpg
- https://caltech-prod.s3.amazonaws.com/main/images/John_Clauser-in-Lab-WEB.max-1400×800.jpg
- https://www.nobelprize.org/images/136227-landscape-medium-gallery-2x.jpg
- https://upload.wikimedia.org/wikipedia/commons/1/1e/Bell-test-photon-analyer.png
- https://images.deccanherald.com/deccanherald%2Fimport%2Fsites%2Fdh%2Ffiles%2Farticleimages%2F2022%2F10%2F04%2Ffen1yaawyaa8u1g-1150664-1664879509.jpg?auto=format%2Ccompress&fmt=webp&fit=max&w=1200
- https://static.timesofisrael.com/www/uploads/2022/07/AP6795987622080007.jpg
- https://static01.nyt.com/images/2014/05/30/science/teleport-1401485477097/teleport-1401485477097-superJumbo.jpg
- https://i.ytimg.com/vi/xthelS-eA3E/maxresdefault.jpg
- https://light2015blogdotorg.files.wordpress.com/2015/09/teleportation.gif
- https://i.stack.imgur.com/zj9KFm.jpg
- https://media.nature.com/lw1024/magazine-assets/d41586-017-07689-5/d41586-017-07689-5_15271308.jpg
- https://www.researchgate.net/profile/Eric-Davis-16/publication/235083700/figure/fig5/AS:299901050212355@1448513390362/Quantum-Teleportation-From-wwwaiporg.png
- https://www.science.org/cms/10.1126/science.1256698/asset/bb32841c-fb61-424d-a17b-a5511bd03b68/assets/graphic/345_510_f1.jpeg
- https://simons.berkeley.edu/sites/default/files/portrait.jpg
- https://freight.cargo.site/w/1250/i/d86b32419921867178526887f653cb1320452f20744d8cf5bafcf9f5ebeb188f/Quantum_Danube_panorama_twin_monuments.jpg
- https://www.esa.int/var/esa/storage/images/esa_multimedia/images/2012/09/laser_from_optical_ground_station_on_tenerife/11655172-7-eng-GB/Laser_from_Optical_Ground_Station_on_Tenerife_pillars.jpg
- https://www.mpq.mpg.de/4887189/PM_12_09_05-1405688917.gif
- https://csis-website-prod.s3.amazonaws.com/s3fs-public/styles/768×461/s3/blog_post/maxresdefault.jpg
- https://global.chinadaily.com.cn/a/202010/26/WS5f960d8ba31024ad0ba80c93.html
- https://www.eoportal.org/api/cms/documents/163813/6202536/QUESS_Auto10.jpeg
- https://www.eoportal.org/api/cms/documents/163813/6202536/QUESS_AutoD.jpeg
- https://upload.wikimedia.org/wikipedia/commons/0/0b/NASA_ISS.png
- https://www.mdpi.com/symmetry/symmetry-14-00997/article_deploy/html/images/symmetry-14-00997-g001.png
- https://www.esa.int/var/esa/storage/images/esa_multimedia/images/2022/10/eagle-1_infographic/24515098-1-eng-GB/Eagle-1_infographic_pillars.jpg
- https://www.esa.int/var/esa/storage/images/esa_multimedia/images/2019/04/saga_for_quantum_key_distribution/19341785-1-eng-GB/SAGA_for_quantum_key_distribution_card_medium.jpg
- https://www.iqoqi-vienna.at/fileadmin/_processed_/e/e/csm_zeilinger_GOD_0686_cd884c215d.jpg
- https://media2.spaceref.com/wp-content/uploads/2023/08/16112240/nanoavionics.png
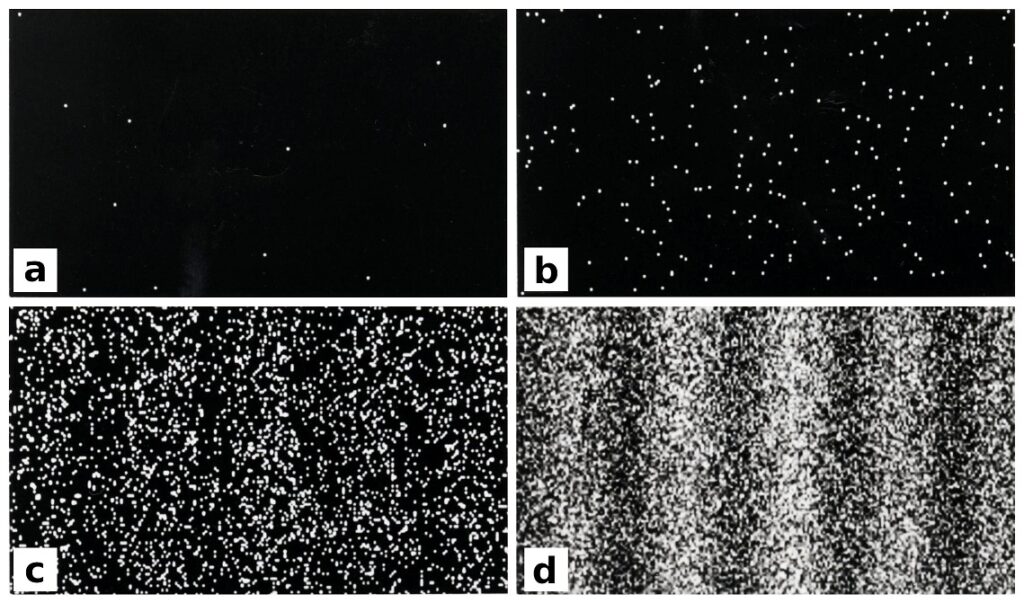





Dík za obsáhlý populární článek. Pro mne úžasný v tom, že srozumitelným způsobem ukazuje cestu, jak dospět k současné domněnce o povaze hmoty a jejích projevů.
Je mi 75. Nesplnitelným přáním by bylo, přečíst si podobný, ale aktuální článek za 100 let.Nebo alespoň zahlédnout tváře studentů čtoucích tento článek za 100 – 200 let.
Vezměte na vědomí, že se právě usmívám.
Pavel Svoboda, skeptik ultra.
Děkuji moc za milá slova.
Mám takový hezký pocit EPR provázání v lidské rovině. Taky mi letos bylo 75 a jako dítě se se těším na každý článek V.Škorpíka, který má vzácný dar shrnout informace v čase i souvislostech. A tak, i když člověk třeba řadu jednotlivých událostí nebo názorů za život zaregistroval, najednou v nich vidí větší řád.
Takže se taky usmívám – a jako OPTIMISTA se těším na všechno nové ve vědě, co ještě stihnu.
Také Vám děkuji za pochvalu, velmi si toho vážím. A doufám, že se ode mne dočtete ještě o mnoha zajímavých novinkách z fyziky.
Naprosto souhlasím s příspěvkem SKEPTIKa.
Úžasný článek pojatý komplexně, ale přitom přiměřeně čitelně. Velice děkuji.
Stav fyziky v půlce 19. století připomíná tehdejšího britského referenta patentového úřadu. Ten se bál o místo, protože vše již bylo vynalezeno.
Také vám moc děkuji za pochvalu.
Moc pěkný článek, zvlášť díky za tu tabulku s orbitaly, nevím, jestli se to dneska ve školách učí, ale mělo by.
Jen poznámku k těm Bellovým nerovnostem:
– neexistuje matematický důkaz, že jsou správně, Bellovo přirovnání k různobarevným ponožkám právě ukazuje, že nechápal důležitost množiny/prostoru, na níž měření probíhá
– pro neeuklidovské prostory lze poměrně jednoduše ukázat „lokální“ proměnnou, která je bude narušovat stejným způsobem, jako kvanta.
Tak určitě, pane fyziku. Všichni fyzikové to mají špatně, ale vy máte samozřejmě pravdu.
Dobrý den,
neexistuje nějaká možnost, jak si tento článek poslechnout v audiu? Třeba pomocí AI?
Dobrý den.
To leda, že bych Vám ho načetl. Ale tím zase budu ztrácet čas k přípravě dalších článků. Tak nevím… Možná se o to můžu pokusit. Nicméně nevím co s obrázky, ty jsou v některých případech zrovna u tohoto článku poměrně důležité.
Díky za skvělý článek. Připomněl mi laboratorní cvičení z fyziky na ČVUT, kde jsem také měřil zde zmíněný experiment s charakteristikou rtuťové výbojky.
Děkuji. A ano, i já jsem v laboratorních cvičeních tento experiment absolvoval. 🙂