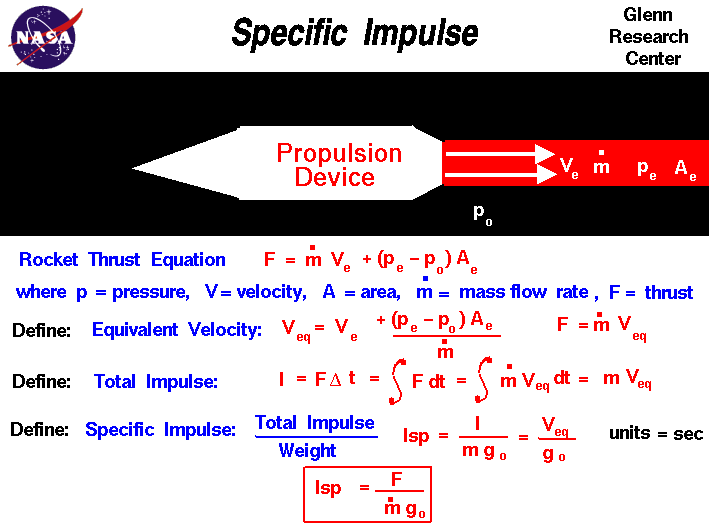
Začátečníci v kosmonautice to mají těžké. Když chtějí do oboru proniknout trochu hlouběji, musí se probrat spoustou složitých definic a termínů, které dokáží snadno zamotat hlavu. Když už nešťastník pochopí jak se to má s těmi apsidami, jak se liší retrográdní dráha od prográdní, vyskočí na něj specifický impuls, u kterého najednou není jasné jak jej uchopit. Další zavaření mozkových závitů se spolehlivě dostaví, když čtenář pozná, že se tento údaj nejčastěji uvádí v sekundách, což je jednotka, kterou by u motoru čekal jen málokdo. Rozhodli jsme se proto vydat nový díl našeho nepravidelného seriálu Pro začátečníky, který se snaží vysvětlovat srozumitelným a názorným jazykem všechna složitá zákoutí kosmonautiky. Dnes si v něm posvítíme právě na záhadně se tvářící specifický impuls. Nenechte se zmást rovnicemi v úvodním obrázku – článek bude mnohem lépe pochopitelný.
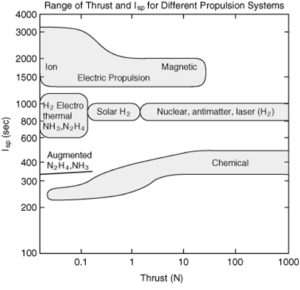
Zdroj: http://www.daviddarling.info/
Tato veličina se v textu může skrývat pod zkratkou Isp, setkat se můžete i s verzí s dolním indexem, tedy Isp a když ji někde uvidíte, můžete vsadit ponožky na to, že bude řeč o raketových motorech. Ba co více, máte co do činění s jedním z nejdůležitějších parametrů, které se točí kolem raketových a proudových motorů. Tento údaj udává palivovou účinnost motoru. No jo, ale co tam v tom případě dělají ty sekundy – může leckdo opáčit. Vtip je v tom, že sekunda není jediná jednotka, ve které může být specifický impuls udáván – k sekundě se v tomto článku ještě vrátíme, ale tím druhým způsobem je N.s/kg. A tady už možná někomu svítá – tato veličina je poměrem tahu, který motor generuje k množství spotřebovaného paliva.
Představme si teoretický motor se specifickým impulsem 600 N.s/kg. Takový údaj znamená, že jeden kilogram pracovní látky (tedy paliva), je schopen vytvořit tah 600 newtonů po dobu jedné sekundy. Platí to i obráceně – jeden kilogram pracovní látky může po dobu 600 sekund vytvářet tah 1 newton. V praxi to samozřejmě tak snadné není, protože každý motor má dané rozmezí, ve kterém je schopen pracovat. Tohle je jedna z věcí, kterou hráči základní verze hry Kerbal Space Program neznají – tam je možné tah motoru lechtat jen na pár procentech, ale ve skutečnosti se motory dají přiškrtit jen na zhruba 40%. Ale zpět ke specifickému impulsu.
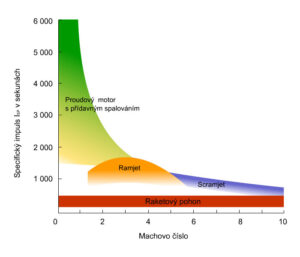
Zdroj: https://upload.wikimedia.org
Už jsme si řekli, že udává palivovou účinnost motoru, tedy jaký tah dokáže získat z určitého množství pracovní látky. Ale když se zamyslíme nad podstatou samotné veličiny, poznáme, že má ještě další tématický přesah. Stačí si jen uvědomit, co je to vlastně tah, který motor produkuje – jde o sílu, která vzniká vypuzováním spalin ze spalovací komory motoru.
A tady se dostáváme ke specifickému impulsu v N.s/kg – jeho číselná hodnota je totiž rovna výtokové rychlosti spalin v metrech za sekundu. To znamená, že náš motor Isp 600 spálí palivo a vytvořené plyny budou mít efektivní výtokovou rychlost 600 m/s. V reálném světě se efektivní výtoková rychlost může od té skutečné lišit, ale to ve skutečnosti příliš nevadí. Efektivní výtoková rychlost, kterou jsme získali ze specifického impulsu totiž můžeme dosadit do Ciolkovského rovnice – vzorce, kolem kterého se točí celá kosmonautika. Je přitom jedno, zda jde o motor s uzavřeným, nebo otevřeným cyklem, zda si nese okysličovadlo s sebou, nebo zda jej čerpá z atmosféry – platí pro motory raketové i proudové.
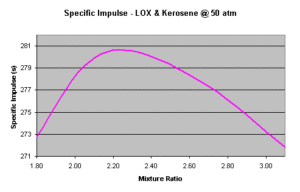
Zdroj: http://www.braeunig.us/
A kde se bere ta sekunda, kterou jsme nakousli na začátku? Za všechno může anglosaská literatura, která specifický impuls chápe trochu jinak – bere ji jako poměr tahu motoru k normálnímu gravitačnímu zrychlení a k sekundové spotřebě. Svým způsobem je to logické – tah i hmotnost můžeme uvádět ve stejných jednotkách – anglosasové mají libry, my kilogramy, ale princip je stejný. Když tedy vidíme specifický tah v sekundách, můžeme z něj vyčíst, jak dlouho (kolik sekund) dokáže jedna libra pracovní látky vytvářet tah jedné libry (to samé platí když vyměníme libru za kilogram).
Verze se sekundou se ale nepoužívá jen v zemích s imperiálními jednotkami, ale i po téměř celém světě, který využívá metrický systém. Výhodou sekundového Isp je, že tato číselná hodnota je po celém světě identická a srozumitelná, tak téměř všichni světoví výrobci udávají ve specifikacích svých výrobků právě sekundovou verzi. Abychom z ní ale získali efektivní výtokovou rychlost, musíme si pomocí násobením gravitačním zrychlením, tedy koeficientem 9,81.
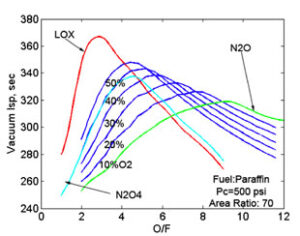
Zdroj: http://www.spg-corp.com/
Verze, která používá N.s/kg se používá prakticky pouze v evropské literatuře a navíc ještě neanglicky psané. Její výhodou je, že je přímo spojena se soustavou SI (což je ale pro anglosaský svět spíše nevýhoda) a hlavně její hodnota přesně odpovídá efektivní výtokové rychlosti a není potřeba zaobírat se vzorcem, kde se násobí gravitačním zrychlením 9,81.
Jak je z minulých vidět, své výhody má jak Isp udávaný v sekundách, tak i udávaný v N.s/kg. Důležité je, že obě verze se mezi sebou dají snadno převádět a že obě mají svůj význam. Doufám, že po přečtení článku už je Vám celá problematika srozumitelnější. Pokud ano, pak náš článek ze série Pro začátečníky splnil svůj úkol a pomohl zdolat jedno z úskalí pronikání do kosmonautiky.
Zdroje informací:
http://mek.kosmo.cz/
https://cs.wikipedia.org/
https://en.wikipedia.org/
http://www.hvezdarna-vsetin.cz/
http://21stoleti.cz/
Zdroje obrázků:
https://www.grc.nasa.gov/www/k-12/airplane/Images/specimp.gif
http://www.daviddarling.info/images2/specific_impulse_for_different_propulsion_systems.gif
http://www.braeunig.us/pics/Isp.gif
http://www.spg-corp.com/images/nytroxperformance_big.jpg


Výborný nápad na článek, teď už tomu konecne rozumím . Tak jste mi udelali radost
A mám taky jednu prosbu-článek o radiokomunikaci (tedy pokud už dříve nevyšel). Vůbec se nevyznám v těch pásmech (Ku, X, S) a třeba tam dát i něco více.
A ještě mě napadá udělat článek o Evropském systemu Galileo.
Ještě jednou díky za vaši práci, moc si jí cením
Těší mne, že článek splnil svůj úkol.
Seriál Pro začátečníky určitě nekončí, rádi do budoucna připravíme další díly. Konkrétně komunikační pásma budou docela oříšek, protože je to hodně specifický obor a pro sepsání takového článku budu muset sám něco nastudovat. Radiotelekomunikace opravdu není můj obor. Ale časem se o to mohu pokusit.
Naopak je velmi pravděpodobné, že v blízké době vydáme článek o evropském systému Galileo. Už brzy totiž bude startovat první Ariane 5, která dokáže vynést rovnou 4 družice najednou.
Přidávám se k prosbě o radiokomunikaci 🙂 Myslím že je to dobrý námět, jednak by mohl pomoci hodně lidem, a jednak je to stejně nezbytná součást kosmických letů jako raketové motory…
Promyslíme to. Přiznám se, že mne zájem o tohle téma docela překvapil.
Něco o systému antén DSN a tím i vesmírné komunikaci se sondami je v češtině i zde:
http://www.fi.muni.cz/usr/jkucera/pv109/2003p/xkolar3.htm
Naopak pane Majer, diskuse o výkonech a dalších parametrech raketových motorů je zde poměrně častá a zatížena mnoha omyly. Tohle je velmi užitečný článek, jeden z těch, který by si měl přečíst každý návštěvník a diskutér tohoto skvělého Kosmonautixu. Já také musím občas obnovit už notně zastaralé školní znalosti a tohle je velmi příjemný způsob.
Díky moc za pochvalu.
Jestli vám pomůže Anglická wiki – tak zde:
https://en.wikipedia.org/wiki/K_band_(IEEE)
https://en.wikipedia.org/wiki/X_band
https://en.wikipedia.org/wiki/Ku_band
https://en.wikipedia.org/wiki/S_band
Asi nepomůže ale díky. Zkusím si to přeložit
Dik za clanok, aj ked je to len preklad, je dobry a zrozumitelny 🙂
Len trocha opravim jeden detail. Imperialne jednotky uz niekolko desatroci nie su zviazane s anglosaskym svetom, pretoze australia a kanada ukoncili prechod na sustavu SI uplne a anglicko je v procese prechodu (zacalo cca 10 rokov neskor). V praxi to ale znamena, ze okrem rychlosti v doprave a niektorych tradicnych mier a vah (potraviny, tabak, atd.) sa u nich vyhradne pouziva SI. Oficialne tak imperialnu sustavu pouzivaju uz len 3 krajiny na svete. Dve su nejake bananove republiky, jedna v afrike, druha v zadnej indii, tretia su spojene staty (aj tam pochybujem, ze sa v kozmonautike s imperialnou sustavou pocita, pretoze je to extremne komplikovane).
Budem ten clovek.
Bohuzial, niektore firmy pocitaju v imperialnych jednotkach napriek kontraktu, a tak sa z Mars Climate Orbiteru stal Mars Climate Impactor. Dokonca konkretne v tom pripade uvadzali hodnoty vo funto-sekundach namiesto newton-sekund, takze islo presne o impulz zazehu.
Specifically, software that calculated the total impulse produced by thruster firings calculated results in pound-seconds.
https://en.wikipedia.org/wiki/Mars_Climate_Orbiter#Cause_of_failure
V USA se samozřejmě v kosmickém průmyslu používá jedině SI soustava. Staré tzv. US customary units se v průmyslu, o vědě nemluvě, čím dál víc nahrazují SI soustavou. Mimochodem mezi britskými imperiálními jednotkami a americkými tradičními jednotkami, tedy US customary units jsou určité rozdíly a není proto obě soustavy dobré zaměňovat. Američané zkrátka imperiální jednotky nepoužívají, ačkoliv z nich ty jejich vycházejí. Navíc dnes je na každém obalu prakticky čehokoliv uváděna hmotnost nebo objem i v kg a litrech. Takže dnes jsou USA v podstatě zemí dvou sytémů. A lidi i postupně se tu učí počítat i v SI jednotkách. Několikrát mě překvapilo, že bez problémů tu někdo dokáže z hlavy převést míle na km.
PS. V USA už víc než měsíc pobývám
Jednu dobu jsem byl mistr na přepočítávání potřeby aut: jejich mpg (miles per galon) na naše litry na sto kilometrů. Fakt zábava.
Jo, hlavně těch několik druhů tun je lahůdka 🙂
Díky za pochvalu, ale nejde tolik o překlad – čerpal jsme především z českých zdrojů.
A díky za detailnější informace o imperiálních jednotkách.
Děkuji za fajn článek. Škoda že v článku není nějaké porovnání Isp několika málo známých motorů, nebo např. porovnání motorů dnešních s motory z počátků kosmonautiky. Člověk by tak získal nejen teoretickou znalost, ale i konkrétní představu. Ale jinak opravdu nanejvýš vhodný článek. Myslím, že dotazy ohledně specifického impulsu se v komentářích objevovaly často.
Přesně tak, posledním impulsem (stylově) byl článek o konstrukci OSIRIS-REx, kde byl specifický impuls zmiňován poměrně často. Rozhodl jsem se tedy článek sepsat. Ohledně porovnání motorů. Dovolím si přidat odkaz na náš starší článek, kde se porovnávají nejrůznější raketové motory a Isp je jedním z parametrů této tabulky.
Wow, perfektní tabulka! Tu jsem tehdy asi přehlédnul nebo už na ni zapomněl. Děkuji za odkaz.
Těší mne, že jsem Vám ji mohl připomenout 😉
Další výborný článek, díky Dušane!
Nevím kam to hodit jinam, tak to píšu sem.. Myslím, že zajímavé téma do této rubriky by bylo zaměřování a telemetrie družic (jak LKO tak meziplanetární sondy). Tzn. jakým způsobem se zjišťuje, že je sonda na správné trajektorii, navíc s tak úžasnou přesností. Ještě jednou díky
Přesně. Za tohle supertéma se taky přimlouvám. Navigace v kosmickém prostoru je úžasná magie.
Skvělé zrovna mě to taky napadlo, jsem rád zle jste to nakousli, též mě to zajímá !!
Uvítal bych taky takový článek, děkuji autorům za povedený web kosmonautix a za jejich práci s publikováním
Díky, popřemýšlíme o tom.
Za téma navigace bych se taky moc přimlouval!
Tím LKO je myšleno co? Low Kerbin Orbit? 😀
Teda 🙂 vůbec mi to nepřišlo špatně, sám s tím mám občas problém.
jezis, a jooo 🙂 to se mi stava porad…
Většina z nás se na LEO nedostane, je tedy potřeba uvažovat v praktičtějších termínech 🙂
Díky za pochvalu, zkusíme časem něco takového udělat, jen neslibuju, kdy to bude.
Na LEO se využívá GPS a Glonas (většina dnešních čipů umí pracovat s kombinací obou systémů) Přesnost je daleko vyšší než na povrchu Země, protože signály nejsou ovlivněny refrakcí v atmosféře. Dále se dají použít laserové dálkoměry atd.
U meziplanetárních sond už je to trochu složitější, tam nic jako GPS není, tam se podle mě bude používat něco na způsob VLBI (doufám že si tu zkratku pamatuji ze školy dobře). Jde o určení směru pomocí triangulace. Sonda vyšle signál k Zemi a ten letí rychlostí světla. Zde ho zachytí několik antén po celém světě a jelikož je naše planeta kulatá tak někde bude dřív a někde později. Máme-li přesně změřené časové odstupy v přijetí signálu a známe-li přesnou polohu antén je už výpočet přesného směru celkem triviální.
Na meziplanetárních sondách by rádiová triangulace moc užitečná nebyla. Maximálně jako doplněk, protože by nebyla přesná (Země je pro sondu jen malá kulička) a informace o aktuální poloze by byla i několik hodin stará.
Používá se triangulace podle hvězd, Slunce a blízkých planet doplněná o inerciální systém. Jak to může fungovat teď, bych si představit dokázal, ale v dobách, kdy se na sondu rozumný počítač nevešel, je mi to záhadou. Podezírám černou magii 😉
Díky za článek, u „N.s/kg“ jsem si řekl „aha“ 🙂
Jedna věc mi jako nadšenému laikovi vrtá hlavou. Trysky motorů mají různou geometrii a u nižších stupňů je vidět (nepřesně označeno) „rozšiřování kužele splodin se vzrůstající výškou“. Nesnižuje to tah motoru?
Variabilní geometrie trysky, jako u proudových motorů stíhaček, není rentabilní/použitelná?
Díky za info.
To rozšiřování trysky je závislé od toho, zda je motor používán v atmosféře, nebo ve vakuu. Variabilní geometrie trysek by byla komplikovaná – motory jsou na jedno použití a navíc by to v některých případech ani nešlo – zvláště u tryskem, které jsou chlazeny regenerativně, tedy trubičkami s palivem.
Myšleno v atmosféře a na její hranici. Tedy to prakticky není rentabilní.
Scott Manley, youtuber, na svém jednom videu udal krásnou historku, jak k tomu došlo, že se Isp uvádí v sekundách. V Ciolkovského rovnici se pracuje jen s výtokovou rychlostí, nic jiného se ve skutečnosti nepotřebuje. Jenomže když Werner von Braun přešel ze svou skupinou Němců do Ameriky zjistil, že se nemohou s americkými inženýry dohodnout na jednotkách rychlosti (m/s vs. ft/s) ani síly (Newtony vs. libry). Pokud však každá strana vydělí výtokovou rychlost ve svých jednotkách, gravitačním zrychlením g ve svých jednotkách vyjde oběma stejné číslo v sekundách (na kterých se už dohodnout dokázali).
Je celkem štěstí, že Isp v sekundách vůbec nějakou interpretaci má a to ještě tak pěknou: „Počet sekund po kterých kilogram paliva dává kilogram tahu.“
Poznámka: Efektivní výtoková rychlost je dobrá jen tehdy když získáváte kyslík z atmosféry (proudové motory) nebo jinak zahrnujete aspekty, se kterými Ciolkovského rovnice nepracuje. U proudových motorů jelikož taháme v raketě jenom zlomek obvyklé hmotnosti paliva, palivo je mnohem účinnější než by napovídala výtoková rychlost (která je stejná). Matematicky to však vychází stejně, jako bychom předstírali, že okysličovadlo bereme sebou, a výtokovou rychlost zvětšily.
Scott Manley je můj oblíbený youtuber, ale tohle video jsem asi minul. Díky moc za rozšíření příběhu.
Pěkná historka.
Ještě bych doplnil, že u proudových motorů vstupují do hry i ostatní atmosférické plyny. Tedy nejen kyslík ze vzduchu a palivo z nádrže. Nasátý dusík (a ostatní plyny), stlačený, ohřátý a vytlačený výtokovou tryskou se nemalou měrou podílí na tahu, i když v podstatě s ničím nereaguje. Proudový motor je tedy ještě mnohem účinnější než hypotetický raketový, kterému bychom nemuseli vézt okysličovadlo.
Máte samozřejmě pravdu. Díky, to jsem si neuvědomil.
To je video Scotta Manleyho: https://www.youtube.com/watch?v=nnisTeYLLgs&index=16&list=PLYu7z3I8tdEn2m_lLL3Vn7BDwkvMLo_hl
Díky moc!
Ale ta interpretace vůbec není „štěstí“. To je prostě fyzika. Pokud lze nějak jednotky podělit, znamená to, že to vždycky bude něco znamenat. Právě to je krása fyziky. S hodnotami lze provádět jen ty operace, které lze provádět i s jednotkami těch hodnot.
Je to spíš zjednodušující konvence. Reálně není Isp v sekundách ani v USA, ale ve zrychlení krát sekunda. Pro Američany je pak tíhové zrychlení Země rovno jedné, tak ho neuvádějí. Něco podobného používají třeba částicoví fyzici – Můžete se dočíst, že hmotnost nějaké částice je xy elektronvoltů, ale elektronvolt je jednotka energie a ne hmotnosti. Striktně by to mělo být xy elektronvoltů lomeno rychlost světla na druhou a právě pro výpočty v kvantové fyzice se často hodí dosazovat za rychlost světla jedničku.
Díky za vysvětlení Vojto, když toto v článku chybělo, jakož i příslušný vzorec s uvedením veličin, kromě u obrázku v úvodu. Ještě mi není úplně jasný ten rozměr N.s/kg.
Vzorec pro specifický impuls je tento:
Isp = F/m.g
a vyjadřuje poměr tahu motoru F k tíze paliva m.
Rozměr Isp je tedy N.s2/kg.m, nikoliv N.s/kg, jak uvádí článek. Leda by se vztahoval ke konstantní rychlosti spalin v (je-li g = v/t, pak Isp = F.t/m.v)
Druhá podoba vzorce u obrázku (pro rozměr času) je:
Isp = Veq/g
Pokud má Veq (ekvivalentní výtoková rychlost) rozměr rychlosti (m/s), pak sekunda jako rozměr vychází. Specifický impuls motoru je tedy dán násobkem ekvivalentní výtokové rychlosti.
Opravuji svůj komentář. Ono je to koukám ještě trochu jinak. To „m“ (s tečkou nad) nebude hmotnost paliva, ale hmotnostní průtok, který má rozměr kg/s, takže výsledný rozměr Isp může být dle vzorce F/m.g avizované N.s/kg, pokud neuvažujeme rozměr konstanty g. Ach ta fyzika!!!
Super vysvětlení, díky
To mne těší, díky!
Přidávám se taktéž k žádosti o článek pojednávající o používaných rádiových pásmech k radiokomunikaci ve vesmíru a se sondami.Bez komunikace na velkou vzdálenost by žádná kosmonautika nebyla a bylo by to zajímavé téma – např. o tom co všechno se musí řešit u meziplanetárních sond kvůli velké vzdálenosti a omezenému výkonu palubního zdroje.
Díky, promyslíme to.
veľmi pekne vysvetlené. Ako ďalšiu tému z raketovej fyziky by som odporúčal propulznú účinnosť reaktívneho pohonu, lebo tá je tiež takou neprechodenou cestou, aj keď má veľký vplyv na konštrukciu viacstupňových rakiet. Vyššia výtoková rýchlosť a tým aj špecifický impulz nemusí byť vždy výhodou, zvlášť na prvých stupňoch, kým sú rýchlosti pohybu relatívne malé voči výtokovej rýchlosti.
Díky za tip!