Zatím jediným způsobem, kterým se nám podařilo poslat sondy k hranicím Sluneční soustavy a získat první informace o mezihvězdném prostoru, byly gravitační manévry při průletu kolem některé z velkých planet naší planetární soustavy. Intenzivně se tato metoda využívá také k zrychlení a zefektivnění cest k jejím různým tělesům. Všech pět pozemských sond, které se zatím vydaly na cestu do mezihvězdného prostoru, využily gravitačního manévru v blízkosti některého z těles Sluneční soustavy. Pomocí správně navrženého těsného průletu v blízkosti planety je možné využít části energie ukryté v oběhu planety kolem Slunce k urychlení sondy vzhledem ke Slunci. Protože planeta má oproti sondě velmi velkou hmotnost, rychlost jejího pohybu vůči Slunci se odebráním energie zmenší zanedbatelně.

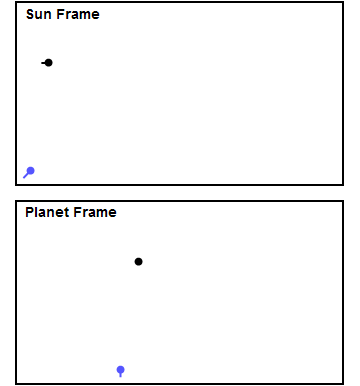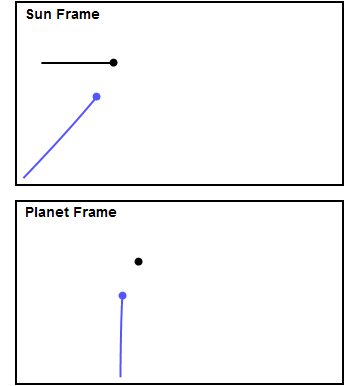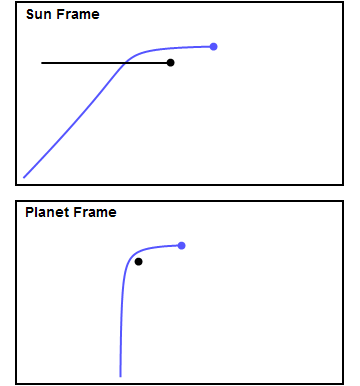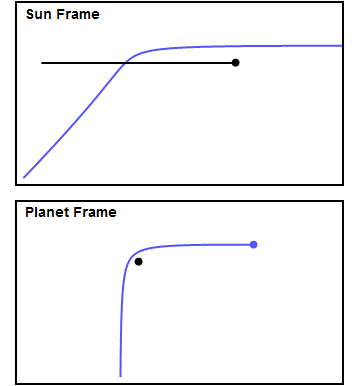
Naopak rychlost sondy vzhledem ke Slunci může narůst značně. Je třeba zdůraznit, že v případě sledování sondy v souřadné soustavě spojené s planetou, kolem které prolétá, bude její dráha hyperbolická a velikost rychlosti vůči planetě bude po průletu stejná. Jak bylo zmíněno, energie, která potřebná ke změně rychlosti sondy vůči Slunci, se odebere z energie spojené s pohybem planety okolo Slunce. Podobným manévrem lze také naopak rychlost sondy vůči Slunci snížit a umožnit jí dosáhnout vnitřní planety Sluneční soustavy.

V případě, že se má sonda vůči Slunci zrychlit, musí proletět za planetou, pokud ji potřebujeme zpomalit, musí proletět před ní (z pohledu směru jejího pohybu po oběžné dráze). Gravitační pole různých těles lze tak pomocí blízkého průletu využít jak ke změně směru tak i velikosti rychlosti letu sondy vůči Slunci a zajistit tak i postupný průletu kolem více těles s případným vysazením malých sond na orbitu kolem těles nebo pro přistání na jejich povrchu. Zbrzdění daleko menšího modulu není tak energeticky náročné.

Aby sonda opustila Sluneční soustavu, musí mít při startu ze Země rychlost větší než zhruba 16,7 km/s. Pokud chceme zajistit nejméně energeticky náročnou cestu sondy ze Země k nějaké planetě, musíme zvolit rychlost u Země takovou, aby se sonda pohybovala po eliptické dráze, která spojuje Zemi a planetu tak, že jedno těleso je v periheliu a druhé v aféliu. Takové energeticky nejvýhodnější dráhy k planetám se označují jako Hohmannovy. Název dostaly podle německého architekta, který je publikoval v roce 1925. Jejich nevýhodou je dlouhá délka letu k jednotlivým planetám. Let k Marsu vyžaduje rychlost startu ze Země 11,6 km/s a vede k trvání letu 259 dní. K Jupiteru je potřebná rychlost 14,2 km/s a let trvá skoro 1000 dní, což je téměř tři roky, let k Plutu potřebuje 16,2 km/s a trval by přes 45 let. Dobu letu lze zkrátit vyšší počáteční rychlostí sondy. Sonda New Horizons tak měla počáteční rychlost 16,2 km/s a k dráze Marsu letěla 70 dní. K Jupiteru, který využila ke gravitačnímu manévru, jí to trvalo 404 dní, tedy něco málo přes rok.

Gravitační manévr v gravitačním poli většího měsíce lze využít i pro usnadnění zaparkování sondy na oběžné dráze planety. V tomto případě dojde předáním části energie sondy měsíci ke změně relativní rychlosti vůči planetě. Tato možnost se nabízí například v případě Jupitera a jeho velkých měsíců nebo Saturna a jeho měsíce Titanu.

V přírodě takové manévry probíhají běžně a ve Sluneční soustavě posílá hlavně Jupiter řadu komet ven ze Sluneční soustavy nebo se naopak řada komet dostane ze vzdálených oblastí našeho hvězdného systému do blízkosti Slunce.

Pravděpodobně prvním člověkem, který se metodou gravitačního manévru zabýval a pochopil její možnosti, byl Guido von Pirquet na přelomu dvacátých a třicátých let. První teoretický rozbor gravitačních manévrů vypracovali v roce 1954 anglický matematik Derk Lawden a na počátku šedesátých let je velice podrobně studovali odborníci z JPL, nejznámější z nich je Michael A. Minovich. Ten popsal své výpočty v interní zprávě v roce 1961, její oficiální publikace se uskutečnila v roce 1963.

Je uváděna i řada dalších jmen, v jejichž pracích se zmínka o této možnosti vyskytla. Jedná se například o práce Jurije Kondraťuka a Friedricha Zandera z dvacátých a třicátých let. V polovině šedesátých let navrhl Garry Flander „Velkou cestu“, při které by mohla sonda díky velmi příznivé konstelaci planet navštívit všechny velké planety a Pluto. Úplně se sice nerealizovala, ale Voyager 2 postupně proletěl kolem Jupiteru, Saturnu, Uranu a Neptunu během pouhých dvanácti let.

Historie realizovaných gravitačních manévrů
Někdy se uvádí, že první gravitační manévr realizovala sonda Luna 3 při svém blízkém průletu okolo Měsíce. Ale zde šlo o neplánovanou záležitost. Urychlení u Jupitera gravitačním manévrem 3. prosince 1973 pomohlo opustit Sluneční soustavu sondě Pioneer 10, která startovala 2. března 1972. I když i v tomto případě nešlo o plánovaný gravitační manévr, který by zajistil cestu k dalšímu cíli. Byla to však první sonda, která se dostala za dráhu Pluta a míří mimo Sluneční soustavu. Poslední signál od ní byl zachycen 23. ledna 2003, kdy byla ve vzdálenosti 80 AU (AU je astronomická jednotka, což je délková jednotka odpovídající zhruba vzdálenosti Země od Slunce, 1 AU = 149 597 870,7 km). Její rychlost je nyní okolo 12 km/s.

Reálnou první planetární sondou, která tento manévr využila k dosažení jiné planety, však byl Mariner 10 vypuštěný 3. listopadu 1973. Ten průletem kolem Venuše 5. února 1974 svoji rychlost snížil a dostal se na dráhu k Merkuru. V témže roce 4. prosince 1974 provedla podobný manévr u Jupitera sonda Pioneer 11, který byl dvojníkem Pioneeru 10, a zrychlila tak svoji cestu k Saturnu. Po průletu okolo něj se vydala na cestu mimo Sluneční soustavu. Automat startoval 6. dubna 1973. V tomto případě se dařilo zachytávat signál ze sondy do roku 1996. Předpokládaná rychlost Pioneeru 11 byla v roce 2015 okolo 11,4 km/s a v polovině toho roku byl ve vzdálenosti okolo 90 AU. Pohybuje se směrem k souhvězdí Štítu a urazí zhruba 2,4 AU za rok.

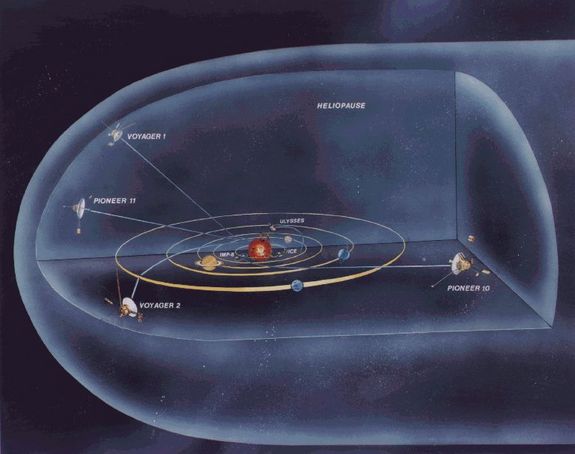
Podobnou cestou do vnějších oblastí se vydaly i sondy Voyager 1 a už zmíněný Voyager 2. Voyager 1 startoval 5. září 1977 a po průletu okolo Jupitera 5. března 1979 se dostal k Saturnu v listopadu 1980. Zde se nakonec vybrala taková dráha, aby umožnila intenzivní studium jeho měsíce Titanu. Sonda se pak vydala k hranicím Sluneční soustavy směrem k souhvězdí Hadonoše. Dne 17. února 1998 dosáhla sonda vzdálenosti 69 AU a předběhla sondu Pioneer 10, její rychlost byla 17 km/s a je nejrychlejší sonda opouštějící Sluneční soustavu. V roce 2012 sonda dosáhla hranice heliosféry. Jako první ze sond začala studovat mezihvězdné prostředí. V polovině roku 2016 byla ve vzdálenosti 135 AU. Za 300 let dosáhne Voyager 1 Oortova oblaku a dalších několik desítek tisíc let mu potrvá, než jim proletí. Signály z něj by mohly být zachytitelné možná ještě okolo deseti následujících let do roku 2035.

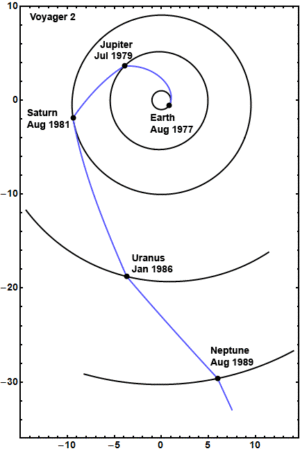
Jak bylo zmíněno, realizoval Voyager 2, který startoval 20. srpna 1977, téměř celou „Velkou cestu“ a postupně proletěl okolo Jupitera, Saturnu, Uranu a Neptuna. Nyní se sonda pohybuje rychlostí 15,4 km/s. Předpokládá se, že bude také dodávat informace možná až deset let.

Sonda Messenger využila gravitační manévr pomocí průletu okolo Země ke snížení rychlosti a cestě k Venuši. Dva gravitační manévry při dvou průletech okolo Venuše ji pomohly dosáhnout dráhy Merkuru. Nakonec ke snížení rychlosti až do takové míry, aby se mohla usadit na orbitě okolo této planety, využila několik průletů a gravitačních manévrů okolo Merkuru.
Gravitační manévry využila při své cestě k Jupiteru také sonda Galileo vypuštěná 18. října 1989. Ta uskutečnila blízký průlet s gravitačním manévrem okolo Venuše a pak dvakrát okolo Země. To umožnilo sondu i s méně výkonným urychlovacím stupněm dopravit k Jupiteru i s dostatkem paliva pro zaparkování na oběžné dráze kolem této planety.
Sonda Ulysses vypuštěná v říjnu 1990 pak využila gravitační manévr při průletu okolo Jupitera v únoru 1992 k dosažení dráhy okolo Slunce velmi vzdálené od ekliptiky, aby mohla studovat polární oblasti naší mateřské hvězdy. Sklon dráhy k ekliptice byl 80,2˚.

Sonda Cassini startující v říjnu 1997 využila na své cestě k Saturnu dva gravitační manévry při těsném průletu okolo Venuše, těsný průlet okolo Země a pak kolem Jupitera. Cesta sondy k Saturnu tak trvala sice o trochu déle než po Hohmannově dráze, ale bylo možné vyslat daleko těžší sondu, než by bylo umožněno pomocí dostupných nosičů.
Čtyři gravitační manévry využila i sonda Rossete, kterou vypustila ESA 2. března 2004 ke kometě 67P/Churyumov-Gerasimenko. Sonda se potřebovala dostat do vnitřní oblasti Sluneční soustavy a toho docílila čtyřmi gravitačními manévry. Blízký průlet okolo Země byl následován velmi blízkým průletem zhruba 250 km nad povrchem Marsu. Nakonec se uskutečnily ještě dva těsné průlety okolo Země. K cílové kometě se sonda dostala v srpnu 2014 a zaparkovala na orbitě okolo ní. Během dlouhého komplikovaného letu proletěla v blízkosti dvou planetek 2867 Šteins a 21 Lutetia a mohla je prozkoumat.

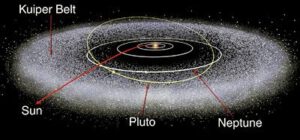
Sonda New Horizons vypuštěná 19. ledna 2006, která 14. července 2015 proletěla okolo Pluta rychlostí 13,7 km/s, využila k získání dostatečné rychlosti k rychlému dosažení svého cíle gravitační manévr u Jupitera. Stává se tak pátou sondou, která opouští Sluneční soustavu. Předtím ji však čeká návštěva některého z těles Kuiperova pásu. Mělo by jít o objekt 2014 MU69. Jeho velikost je 30 až 45 km a oběžná perioda 293 let. Průzkum vnějších oblastí Sluneční soustavy je důležitý i z hlediska mezihvězdných letů. Ať už z hlediska možných základen, zdrojů surovin nebo možných rizik. Pak bude sonda následovat sondy Pioneer a Voyager a bude zkoumat hranici heliosféry a přechod slunečního prostředí v mezihvězdné.

Je vidět, že gravitační manévr se během historie zkoumání Sluneční soustavy poměrně intenzivně využíval. Řadě sond umožnil se dostat k jednomu nebo i více tělesům Sluneční soustavy. Celkově pět sond pomocí něj Sluneční soustavu opouští. Jejich rychlost se pohybuje mezi 11 až 17 km/s. Během jednoho roku tak urazí vzdálenost zhruba v intervalu mezi 2 až 4 AU. Všechny sondy zůstávají ne tak daleko od roviny ekliptiky. Pioneer 10 letí do směru v blízkosti souhvězdí Vozky, Pioneer 11 je pak ve směru mezi souhvězdími Hadonoše a Kozoroha, Voyager 1 pak mezi souhvězdími Pastýře a Hadonoše a Voyager 2 pak letí směrem k souhvězdí Tukana. Sonda New Horizons je nyní ve směru souhvězdí Střelce.

Celková dosažená rychlost je limitována možností co nejbližšího průletu kolem planety, tak aby sonda nevnikla do její atmosféry. Pokud chceme využít více gravitačních manévrů u více těles, jsme silně závislí na jejich vzájemné poloze. Například další „Velká cesta“ bude realizovatelná až v polovině 22. století. A to už budou raketové pohony na takové úrovní, abychom byli schopni cestovat k vnějším planetám rychleji bez využití těchto manévrů.

Pokud by mezihvězdná loď chtěla změnit svoji rychlost vůči galaktickém centru a změnit směr letu, může provést gravitační manévr těsným průletem okolo Slunce, případně naše sondy mohou provést podobný manévr u jiných hvězd. Taková situace je popsána v knize Arthura Clarka „Setkání s Ramou“.

Možnost většího zrychlení při gravitačním manévru
Pro zesílení účinku gravitačního manévru lze využít Oberthův efekt. Ten spočívá v tom, že změna rychlosti kosmické sondy pomocí raketového motoru je tím vyšší, čím rychleji se sonda pohybuje. Efekt je způsoben tím, že palivo už má v této situaci nějakou kinetickou energii. Jeho aplikací se například dosahuje toho, že využití paliva ve vyšších stupních rakety je efektivnější. V našem případě je tak velmi výhodné provést motorický manévr při průletu sondy v místě nejbližšího přiblížení k tělesu, kdy má sonda rychlost nejvyšší. Spojením vhodného gravitačního a motorického manévru tak můžeme docílit významné změny rychlosti. Tento případ se často označuje jako Oberthův manévr. Oberthův manévr lze na rozdíl od čistého gravitačního manévru uskutečnit i blízkým průletem okolo Slunce s využitím velmi vysoké rychlosti v periheliu.

Gravitační manévry využívající planety Sluneční soustavy, byť zesílené uplatněním Oberthova manévru sice umožní vyslat sondy ke hvězdám, ale pouze rychlostmi, které jsou v řádu stovky kilometrů za sekundu, tedy velmi malé oproti rychlosti světla. Cesta k nejbližším hvězdám tak potřebuje řádově tisíce až desetitisíce let. Velice zajímavé využití této metody, které umožňuje získat rychlosti blížící se procentům či dokonce desítkám procent rychlosti světla, navrhl fyzik Freeman Dyson z univerzity v Princetonu již v roce 1963. Rychlosti blízkých rychlosti světla by bylo možné v principu dosáhnout při průletu kolem kompaktního tělesa v těsném binárním systému. Tedy systému složeného ze dvou neutronových hvězd, černých děr, nebo kombinace těchto těles případně také bílého trpaslíka a některého z kompaktnějších těles. Pro menší urychlení stačí i vhodná dvojhvězda složená z bílých trpaslíků. Pochopitelně, že by nejdříve bylo potřeba takový systém najít a také se k němu s případnou mezihvězdnou lodí dostat.

Nemalé rychlosti lze dosáhnout i v systému dvou bílých trpaslíků. Pokud budeme mít systém složený ze dvou bílých trpaslíků o hmotnosti Slunce a odpovídajícím poloměru srovnatelném s poloměrem Země, které mají oběžnou periodu okolo 100 s, můžeme při využití vhodné dráhy získat rychlost až okolo 1 % rychlosti světla. Ovšem pro dvojhvězdu složenou ze dvou neutronových hvězd, které mají zhruba poloměr 10 km, hmotnosti v řádu hmotnosti Slunce a orbitální periodu okolo 0,005 lze dosáhnout rychlosti přesahující čtvrtinu rychlosti světla.

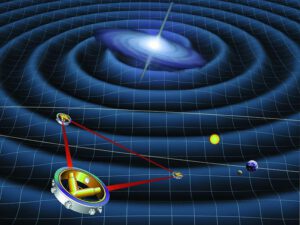
Nalezení vhodného dvojhvězdného systému může být velice těžké, protože svítí minimálně. Důležitý krok k tomuto úkolu se uskutečnil v roce 2016, kdy se poprvé pomocí interferenčního detektoru LIGO podařilo zachytit gravitační vlny vzniklé při splynutí dvou černých děr (viz zde a zde). V tomto případě jde o záznam konce takového systému, i když jsme tím získali informaci o existenci velmi hmotné černé díry, která se alespoň ve sci-fi k mezihvězdnému cestování hodí také. Zatím je problémem, že sice známe zhruba vzdálenost objektu (ta je velmi velká – 1,3 miliard světelných let), ale neznáme směr, ve kterém se nachází. To by se již brzy mělo změnit. Jakmile začne pracovat také vylepšený detektor VIRGO a indický třetí detektor LIGO, který se začal budovat v Indii, dostaneme daleko přesnější informaci o poloze velkých černých děr vznikajících splynutím dvojhvězdných systémů. Tato sestava detektorů by nás měla pravidelně zásobovat stále novými černými děrami.

Budoucí systémy, jako je japonská podzemní KARGA nebo později vesmírný systém eLISE, umožní pozorovat gravitační vlny na jiných frekvencích. To by mělo dovolit pozorování systémů dvojhvězd složených z černých děr před splynutím a také tvořené neutronovými hvězdami nebo kombinací těchto objektů. Neutronové hvězdy je možné ve specifických případech pozorovat už nyní. To jsou ty případy, kdy Zemi zasáhne kužel elektromagnetického záření hlavně v rádiovém oboru vyzařovaný ve směru její magnetické osy a neutronovou hvězdu pozorujeme jako pulsar. Ovšem takových případů, kdy je kužel záření směrován k Zemi, je málo a se stářím neutronové hvězdy signál pulsaru slábne. I z toho důvodu nám velký počet binárních systémů neutronových hvězd zůstává utajen a právě ty nejbližší by nám mohl pomoci odhalit vhodný detekční systém gravitačních vln. Pokud vyřešíme problém, jak se dostat k prvnímu z nich, mohla by ve vzdálené budoucnosti mapa jejich poloh vyřešit putování mezi hvězdami i na velmi velké vzdálenosti.

Pokud se podaří pomocí gravitačního detektoru zjistit blízkou černou díru, existuje ještě jedna možnost urychlení sondy na rychlost blízkou rychlosti světla. A to využití těsného průletu okolo černé díry. Je třeba zdůraznit, že i v této situaci se získá energie pro změnu rychlosti z pohybové energie tělesa, v jehož gravitačním poli sonda manévr provádí. V tomto případě sonda odebere zanedbatelnou část rotační energie černé díry a zanedbatelně její rotaci zpomalí. Je tak jasné, že se musí jednat o rotující černou díru, která se označuje jako černá díra Kerrova. Protože nejspíše všechny hvězdy rotují a mají moment hybnosti, měly by vzhledem k zákonu zachování hybnosti rotovat i všechny reálné černé díry vzniklé kolapsem na konci života velmi hmotných hvězd. Vhodným průletem těsně nad horizontem černé díry tak lze získat i rychlosti velmi blízké rychlosti světla. Sonda nesmí v tomto případě spadnout pod horizont, ale musí se dostat dovnitř ergosféry. To je oblast existující nad horizontem u rotující černé díry, kde dochází k velice intenzivním efektům strhávání časoprostoru ve směru rotace.

Pro získání energie se využije tzv. Penroseho proces publikovaný Rogerem Penrosem v roce 1963, který kromě urychlování sond umožňuje i čerpat energii z rotace černé díry. Je však třeba také obětovat část hmotnosti hvězdné lodě. Obětovaný materiál se pošle pod horizont černé díry a zvětší její hmotnost. Naopak se zvýší kinetická energie lodě a to o hodnotu, která představuje velkou část klidové energie odvrženého materiálu. Lze tak získat urychlení až na rychlosti blízké rychlosti světla. Takové urychlování pravděpodobně pozorujeme ve formě výtrysků pozorovaných u černých děr, například v případě kvazarů. Kromě otázky nalezení vhodné černé díry a dopravy k ní by bylo nutné vyřešit i konstrukci sondy, která by takový průlet a urychlení přežila. Jak bylo zmíněno, zpomalí se urychlením lodě rotace černé díry, ale jen o zanedbatelně malou hodnotu.

Pokud by se popsané metody gravitačního manévru využívající binární systémy nebo jednotlivá kompaktní konečná stádia hvězd podařilo realizovat a získala se mapa těchto objektů v našem okolí, dala by se skoky od jednoho k druhému postupně stále více zvyšovat rychlost sondy. Je však třeba zdůraznit, že vzdálenost k nejbližším vhodným objektům bude spíše stovky až tisíce světelných let. Případné uskutečnění takové možnosti, pokud je vůbec realizovatelná, je tak hodně vzdálené.

Touto možností jsme se pomalu dostali na hranici současné fyziky. Všechny umožňují pouze cesty rychlostí nepřesahující rychlost světla. Všechny další možnosti, které souvisí s gravitací a prostoročasem, například průlet černou dírou a využití červí díry nebo různé formy warp pohonu jsou už mimo ní a alespoň zatím jsou čistě v oblasti spekulací a fantastiky.

Závěr
Jak je vidět z přehledu, je řada možností, jak využít průlet gravitačním polem nějakého tělesa k urychlení vesmírné lodě. Gravitační manévr při průletu okolo velkých planet sluneční soustavy je zatím jedinou metodou, která nám umožnila poslat sond k hranicím Sluneční soustavy. Pět průzkumníků tak putuje ven ze Slunečního systému do mezihvězdného prostoru. Tato metoda by nám už nyní umožnila s využitím Oberthova manévru nebo v kombinaci se sluneční plachetnicí, o které se zde psalo nedávno, a iontovým motorem vyslat těžší sondu v rozumném čase na kraj Sluneční soustavy a prozkoumat detailně vlastnosti mezihvězdného prostoru.

Už dnes nám také velice sofistikovaně navržené gravitační manévry ulehčují cestu k různým objektům Sluneční soustavy. Je předpoklad, že intenzita jejich využívání v budoucnu poroste.

V klasickém případě však gravitační manévr neumožňuje dosažení takové rychlosti, aby se byť k nejbližším hvězdám mohlo dospět za rozumnou dobu. Takové rychlosti lze dosáhnout pouze v kombinaci s jinými pohony nebo s využitím velice exotických systémů složených z kompaktních konečných stádií hvězd.

Praktické využití těchto možností je velmi vzdálené a nejisté. Prozatím však lze v nejbližších letech čekat zlom v identifikaci a nalezení takových objektů pomocí detektorů gravitačních vln. A případně začátek vytváření mapy budoucího mezihvězdného putování. Lze doufat, že půjde o podobný zlom na naší cestě k hvězdné budoucnosti podobný tomu, jakým bylo rozvinutí metod identifikace exoplanet (viz zde).

Článek vyšel na osel.cz.