Nestává se často, abychom na Kosmonautixu mohli informovat o natolik přelomové skutečnosti, jako mám tu čest učinit dnes. Měření vzdáleností v kosmu je velmi obtížná disciplína. Naše měření dosud končila u známých supernov Ia, na které se ovšem nemůžeme spoléhat ve vesmíru mladším než 5 miliard let. Pro měření na těchto vzdálenostech potřebujeme jiný referenční zdroj.

Kvasary jsou samy o sobě fascinující objekty vyskytující se pohříchu zejména ve velmi hlubokém vesmíru. Pravděpodobně se jedná o supermasivní černé díry přitahující nezměrná množství materiálu, z něhož podstatnou část nakonec ani nespolykají a vyvrhují ho zpět do okolí zejména v podobě polárních výtrysků a záření. Dnes však necháme nejbizarnější vlastnosti kvasarů stranou. Bude nás zajímat, zda je můžeme využít k měření vzdáleností ve vesmíru. Dosud jsme pro největší vzdálenosti měli k dispozici pouze supernovy Ia, které díky své povaze definované fyzikou platnou univerzálně v celém vesmíru lze dobře využít jako standardní svíčky, jenže těch ve vesmíru mladším než 5 miliard let není moc. Proto Guido Risaliti a Elisabeta Lusso z Arcetri Astrophysical Observatory Firenze navrhují dosavadní metodiku rozšířit právě o kvasary, které v těchto vzdálenostech pozorujeme ve velkém množství. Využili k tomu závislost absolutní magnitudy kvasaru (tedy skutečného zářivého výkonu, nikoli zdánlivé magnitudy na pozemské obloze) na poměru mezi vyzařováním v ultrafialovém a rentgenovém oboru. Tuto závislost astronomové tušili již od roku 1970, jenže až v posledních deseti letech bylo možné sestavit dostatečný vzorek čítající 1138 kvasarů se známým vyzařováním v obou oborech, aby bylo možné tuto závislost určit a také ověřit její platnost ve všech epochách vývoje vesmíru. Dlužno podotknout, že většina použitých údajů pochází z observatoře ESA XMM-Newton. Měření kvasarů je sice méně přesná metoda než známé supernovy Ia, ale co dělat, když zvláště na vyšším rudém posuvu jich je na rozdíl od supernov k dispozici dostatek. Síla nového přístupu se naplno projevila v kombinovaném pozorování 13ti miliard let kosmické evoluce pomocí supernov Ia a kvasarů. Využití obou metod umožnilo omezit relativní poměr temné hmoty a temné energie přesněji než by to umožnilo samotné pozorování supernov.

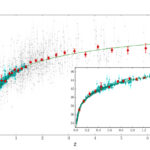
Graf vlevo ukazuje, jak můžeme využít měření vzdálených astronomických objektů ke studiu expanzní historie vesmíru. Graf zobrazuje závislost rudého posuvu a modulu vzdálenosti více než tisíce astronomických zdrojů. Na vodorovné ose vidíme rudý posuv (z), na svislé ose modul vzdálenosti objektu. Modré body reprezentují supernovy typu Ia. Šedé body představuj kvasary využité jako standardní svíčky na základě vztahu svítivosti a poměru emisí v ultrafialových a rentgenových vlnových délkách. Červené body ukazují průměrné hodnoty několika kvasarů s podobným rudým posuvem.

Nová metoda si v každém případě zaslouží práci na dalším zpřesňování, o které si množstvím vhodných objektů sama říká. ESA zamýšlí k tomuto účelu v blízké budoucnosti využít přístroj eROSITA, umístěný na palubě ruské observatoře Spektr-RG, v dlouhodobějším výhledu se očekávatelně zapojí ATHENA. Mezitím se dostane ke slovu i dalekohled Euclid, ten sice bude pracovat ve viditelné a blízké infračervené oblasti, ale UV záření některých kvasarů může být díky kosmologickému rudému posuvu posunuto až do jeho vlnových délek. Osobně si dovolím vyjádřit soukromé přání, aby se i JAXA postavila k věci vstřícně a poskytla k tomu účelu nějaký pozorovací čas na chystané observatoři ASTRO-H, nechme se překvapit.

Vzhledem k dnešnímu tématu považuji za vhodné alespoň v kostce připomenout tzv. kosmologický žebřík. Čtenář znalý tohoto konceptu může následující řádky směle vynechat.

Paralaxa – princip je využitelný pro nejbližší hvězdné sousedství do vzdálenosti maximálně ve stovkách ly. Metodu lze snadno demonstrovat, když budeme pozorovat třeba vztyčený prst a střídavě zakrývat jedno a druhé oko – prst se vám bude promítat na různá místa pozadí. U hvězd to pochopitelně nefunguje tak jednoduše, ale stačí počkat půl roku, než se Země posune na opačnou stranu Slunce, aby bylo v silách techniky vzniklou paralaxu měřit. Roli prstu tu bude hrát blízká hvězda. Budeme měřit její posun vůči mnohem vzdálenějším objektům v pozadí.

HR diagram – z klasické fyziky víme, že těleso vidíme tím slabší, čím je vzdálenější, přesněji:  jeho jasnost klesá s druhou mocninou vzdálenosti. Tato zákonitost platí i pro hvězdy. Je zjevné, že pro využití tohoto principu musíme znát svítivost hvězdy. Pokud prozkoumáme blízké hvězdy z pohledu jejich povrchové teploty a svítivosti, pak po vynesení těchto hodnot do grafu zjistíme, že jejich rozložení není náhodné. Ze znalosti povrchové teploty lze tedy určit absolutní svítivost hvězdy a následně na základě její jasnosti dopočítat vzdálenost. Tato metoda je zcela dostatečná v rámci naší Glaxie, tj. na vzdálenosti do 100 000 ly.

Cefeidy – Pokud chceme znát vzdálenost nějaké sousední galaxie, například Andromedy,  musíme přijít s něčím ještě lepším. Tím „něčím“ se díky jisté Henriettě Swan Leavittové ukázaly být proměnné hvězdy. Dotyčná dáma, svého času zaměstnaná na Harvard College Observatory, objevila vztah mezi periodou proměnných hvězd zvaných Cefeidy a jejich svítivostí. Tím byla zavedena první standardní svíčka v astronomii.

Supernovy Ia – jsou druhá standardní svíčka, kterou ve vesmíru máme. Jedná se o zvláštní typ supernovy, kdy vybuchuje bílý trpaslík, který na svůj povrch strhává hmotu svého většího souputníka. K výbuchu dochází v okamžiku, kdy hmotnost bílého trpaslíka uvedeným způsobem naroste na 1,44 hmotností Slunce – tzv. Chandrasekharova mez. Po jejím dosažení se na jeho povrchu zažehne překotná termonukleární syntéza hélia a celý trpaslík je rozmetán do okolí za vzniku působivých mlhovin. Protože k tomu dochází vždy za stejných okolností, mají tyto výbuchy vždy tentýž průběh i stejnou absolutní jasnost, a proto lze měřením jejich zdánlivé jasnosti určit jejich vzdálenost.

Rudý posuv – tato příčka pomyslného žebříku vychází ze skutečnosti, že náš vesmír se jako celek rozpíná. Z toho plyne, že velmi vzdálené objekty se od sebe musí vzdalovat, a to tím rychleji, čím jsou vzdálenější. Celá situace bývá přirovnávána k pravidelně rozmístěným tečkám na nafukujícím se balónku: dvě sousední tečky se vždy budou při jeho nafukování vzdalovat, přičemž ty vzdálenější se od sebe budou vzdalovat rychleji. Je tedy zjevné, že z jejich vzájemné rychlosti lze zpětně dopočítat vzdálenost, která je dělí. Stejně tak to lze provést i pro velmi vzdálené galaxie ve vesmíru. Rychlost objektu vůči pozorovateli dovedeme snadno zjistit pomocí Kosmologického rudého posuvu. Má to ale háček: přesnost výpočtu silně závisí na přesné znalosti poměru mezi rychlostí vzdalování a vzdáleností – Hubbleově konstantě. A protože hodnotu Hubbleovy konstanty určujeme na základě výše uvedených metod, není to úplně ono. Proto považuji novou kvasarovou metodu za hodnou bližší pozornosti.

Zdroje informací:
http://phys.org/
http://sci.esa.int/

Zdroje obrázků:
http://sci.esa.int/.../Risaliti_Lusso_Universe_gauge_625w.jpg
http://sci.esa.int/science-e-media/img/9a/An_X-ray_view_of_the_COSMOS_field_625w.jpg