Minulý článek o výpočtu rychlosti družice na oběžné dráze kosmického tělesa sklidil u čtenářů docela velký úspěch. Není se co divit, kosmonautika je obor, který se matematice vyhnout nemůže. Přesto může být, především pro některé nováčky v oboru, docela komplikované do tohoto rozjetého vlaku naskočit. Dnes proto přichází další díl našeho seriálu, který cílí právě na nové zájemce o kosmonautiku. Zaměříme se na změnu rychlosti na oběžné dráze a stejně jako v minulých dílech, i tentokrát budeme všechno vysvětlovat pomalu a názorně.
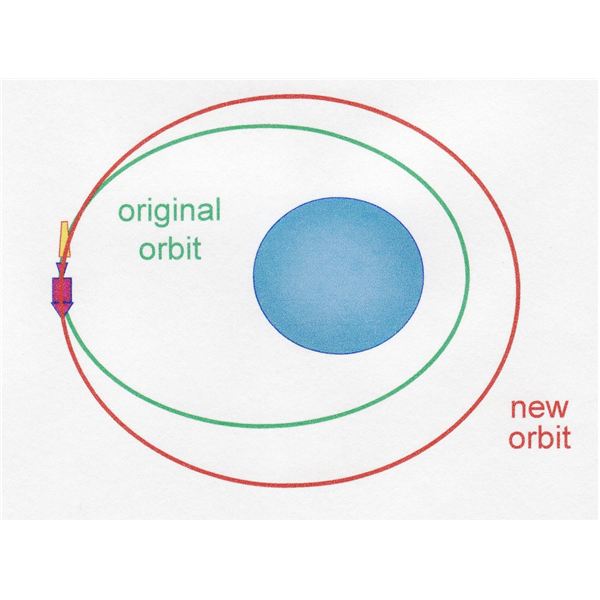
Změny rychlosti na oběžné dráze jsme lehce nakousli už v tomto díle. Už tedy víme,že každá oběžná dráha je eliptická a že na ní najdeme dva body, kterým říkáme apsidy. V apoapsidě je družice nejdále od centrálního tělesa (planety/měsíce/hvězdy) a má vůči němu nejnižší rychlost. Naopak v periapsidě má rychlost nejvyšší a je tělesu nejblíže. Pokud chceme vzdálit polohu jedné apsidy od centrálního tělesa, musí družice zažehnout svůj motor v protilehlé apsidě a pozor – ve směru letu! Jinými slovy – satelit musí zrychlit. Pokud naopak chceme snížit polohu apsidy, musíme i tentokrát zapálit motor v protilehlé apsidě, tentokrát ale proti směru letu. Družice tedy zpomalí, což ovlivní polohu protilehlé apsidy.
Tolik tedy základní průprava do problematiky apsid.Nyní už můžeme přikročit k hlavnímu obsahu článku, tedy k výpočtům. V minulém díle jsme se naučili, jak můžeme vypočítat aktuální rychlost tělesa na oběžné dráze.
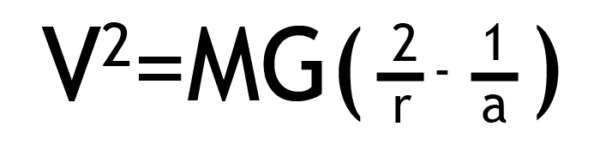
Zdroj: Autor
Jen pro pořádek připomenu, že velká poloosa dráhy je aritmetický průměr z vzdáleností obou apsid od těžiště centrálního tělesa. V dnešním článku se naučíme další termín, se kterým se při výpočtech pracuje velmi často a sice Δv [delta vé]. Tento údaj označuje změnu rychlosti družice, tedy o kolik m/s musí zpomalit, nebo zrychlit, aby se dostala na požadovanou dráhu. Pojďme tedy na první slovní úlohu. Máme družici, kterou nosná raketa vynesla na dočasnou parkovací dráhu ve výšce 300 kilometrů nad Zemí. Potřebujeme ji dopravit na téměř kruhovou dráhu ve výšce 35 800 km. Jakou rychlost musíme družici dodat, jaké tedy bude Δv?
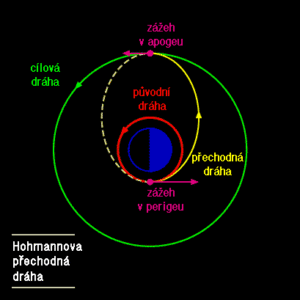
Zdroj: http://www.nels.pwp.blueyonder.co.uk/
Překlad: Autor
Jak budeme při výpočtu postupovat? Nejprve si celou situaci představíme. Družice bude přecházet z jedné téměř kruhové dráhy na druhou téměř kruhovou. To znamená, že změní polohu obou apsid. Z toho vyplývá, že takovou změnu není možné udělat pouze jedním zážehem – tím se mění poloha vždy jen jedné apsidy. Budeme tedy potřebovat zážehy dva. První, který nám z původní kruhové dráhy udělá eliptickou a vytáhne apoapsidu do výšky geostacionární dráhy. Druhý zážeh pak přijde v apoapsidě a zvýší periapsidu = zakulatí oběžnou dráhu.
Nyní, když už máme všechny potřebné teoretické základy, přistoupíme k výpočtu, který známe už z minulého dílu našeho seriálu. Vypočítáme si rychlost družice na téměř kruhové oběžné dráze ve výšce 300 km nad Zemí.
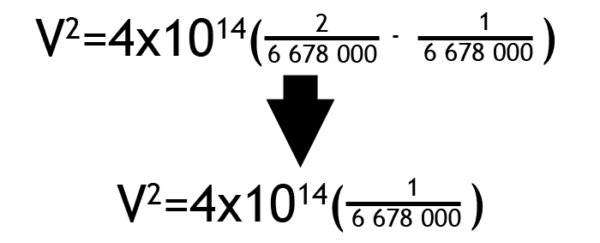
Zdroj: Autor
Nyní víme, že těleso se na této téměř kruhové dráze pohybuje rychlostí 7 739 m/s. Tohle číslo si zapíšeme a na chvíli jej opustíme. Nyní se zaměříme na stav po prvním zážehu, kdy jsme vytáhli apoapsidu do výšky 35 800 km nad povrch Země. Vypočítáme si teď rychlost družice v periapsidě této eliptické dráhy, která zůstává 300 km nad Zemí. Připomínám, že ke všem vzdálenostem je nutné přičíst poloměr naší planety 6 378 km. Velká poloosa této oběžné dráhy je tedy 24 428 000 metrů (průměr z 42 178 a 6 678).
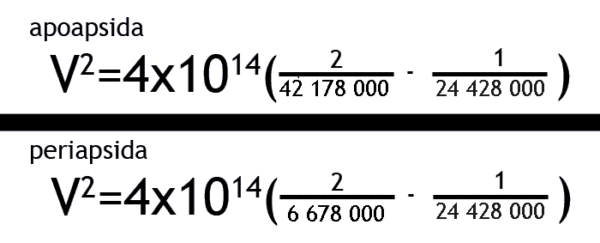
Zdroj: Autor
Pokud vypočítáme výše zobrazený vzorec, vyjde nám, že v periapsidě bude rychlost 10 169 m/s a v apoapsidě 1 610 m/s. Všimněte si, jak výrazně se obě rychlosti liší. Je to kvůli tomu, že dráha je extrémně protáhlá. Nyní se vrátíme k číslu, které jsem si před chvílí dočasně odložili – rychlost na kruhové dráze ve výšce 300 km byla 7 737 m/s. Na současné eliptické dráze vzrostla na 10 169 m/s. Pokud od sebe obě hodnoty odečteme, dostaneme se na hodnotu 2432 m/s. To je hodnota Δv, tedy změna rychlosti potřebná pro přechod z kruhové dráhy ve výšce 300 km na eliptickou dráhu. Tím ale naše výpočty nekončí.
Naším úkolem je vypočítat změnu rychlosti potřebnou pro dosažení kruhové dráhy ve výšce 35 800 km. A na ní zatím nejsme. Zatím jsem dosáhli pouze dráhy eliptické. Nyní musí naše družice zapálit svůj motor v apoapsidě, vytáhnout nahoru periapsidu a zakulatit svou dráhu. Potřebujeme tedy vypočítat, jaká bude rychlost družice na finální dráze. Jelikož se jedná o téměř kruhovou dráhu, můžeme použít zjednodušený výpočet, který jsme si představili v minulém díle, tedy V2 = μ / a. Po dosazení nám vyjde, že se družice na této dráze pohybuje rychlostí 3 079 m/s. Družice na eliptické dráze tedy musí v nejvyšším bodě zrychlit právě na tuto rychlost, aby zakulatila svou oběžnou dráhu.
Pokud od sebe odečteme tuto rychlost a dříve vypočítanou rychlost v apoapsidě (1 610 m/s), dojdeme k výsledku 1 470 m/s. Tato rychlost je potřebná, aby satelit zakulatil svou oběžnou dráhu. Známe tedy Δv pro druhý zážeh. Abychom vypočítali celkové Δv, sečteme obě doposud vypočítané hodnoty, tedy 2 432 m/s a 1 470 m/s a vyjde nám celkové Δv, přesně 3 902 m/s. Úlohu jsme tedy vyřešili – Družice potřebuje pro přechod z kruhové oběžné dráhy ve výšce 300 km na kruhovou dráhu ve výšce 35 800 km celkové Δv 3 902 m/s.
Možná vás zaujalo, jak výrazně se od sebe liší obě Δv, které jsme spolu sčítali. Jak je možné, že vytahování apoapsidy z kruhové dráhy na eliptickou potřebuje změnu o 2432 m/s, zatímco vytahování periapsidy, tedy zakulacování dráhy jen o 1710 m/s? Důvod je prostý – musíme vzít v úvahu vzdálenost místa, kde zážeh provádíme od Země. Jinými slovy – čím jsme od centrálního tělesa dál, tím slabší je v těchto místech jeho gravitace, proti které musíme bojovat. Malá změna Δv provedená ve velké vzdálenosti od centrálního tělesa tak přinese velkou změnu protilehlé apsidy.
Ještě je ale potřeba upozornit na jednu velmi důležitou věc. Všechna čísla, která takto vypočítáme jsou zatížena nepřesností. Jde o to, že výsledky, které nám vyšly počítají s nereálnou situací, kdy družice zapálí přesně v apsidě svůj motor na nekonečně krátký čas a okamžitě dosáhne požadované rychlosti. V reálu tomu tak ale není – zážehy trvají několik desítek sekund, často i minuty. Motor se tedy musí zapálit ještě než družice proletí apsidou a musí hořet i potom. Jenže pokud motor hoří mimo apsidu, není už zážeh tolik účinný.
To je ostatně důvod, proč indická sonda Mangalyaan odlétala k Marsu postupně. Několika kratšími zážehy postupně protahovala svou oběžnou dráhu, protože neměla k dispozici silnější motor, který by byl schopný ji urychlit za kratší čas. A kdyby se zážeh neúměrně protahoval, musel by motor hořet i daleko od apsidy, což by nebylo tolik výhodné. Indové proto sáhli k elegantnímu řešení, kdy potřebný zážeh rozdělili na několik menších, které byly prováděny ve větší blízkosti apsidě, takže byly mnohem účinnější.

Zdroj: http://media2.intoday.in/
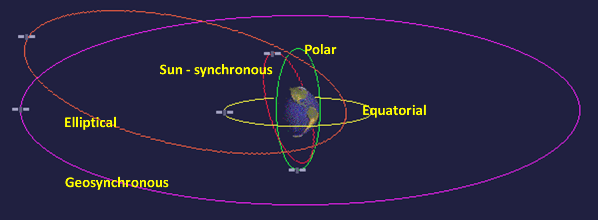
Pozorní čtenáři si jistě všimli jedné zajímavé věci – dopravovali jsme sice družici na výšku geostacionární oběžné dráhy, ale nebrali jsme v úvahu sklon dráhy. Geostacionární dráha totiž s rovníkem svírá nulový úhel. Jelikož jsou kosmodromy umístěné mimo rovník, musí satelit provádět i korekce sklonu oběžné dráhy. Ale to si necháme až na další díl našeho nepravidelného seriálu. V něm vypočítáme, jaké Δv potřebuje skutečná telekomunikační družice, aby se dostala na geostacionární dráhu, naučíme se počítat Δv pro změnu sklonu oběžné dráhy.
Zdroje informací:
http://www.youtube.com/
http://cs.wikipedia.org/
http://en.wikipedia.org/
Zdroje obrázků:
http://img.bhs4.com/…FDAD6D7FF1A59C7738E2E5E0B7_large.jpg
http://www.nels.pwp.blueyonder.co.uk/GURPS/THS/Hohmann.gif
http://media2.intoday.in/…/mars_660_112913064922_120313115916.jpg





Nadherne citanie na rano, vdaka.
Dugi tak tento článok je naozaj luxus :). Takto jednoducho vysvetlená orbitálna mechanika 🙂 . Priznám sa že väčšinu základov ma naučil Kerbal Space Program ale nikdy som nevedel ako to vlastne funguje keďže vždy keď som sa snažil nájsť nejaké vzorce k orbitálnej mechanike tak na mňa vyskočili vzorce na úrovni vysokoškolskej matiky 😀
Tak to mám radost. Jelikož matika taky nepatří k mým oblíbeným oborům, snažím se ji předkládat srozumitelně. Těší mne, že se to daří. 🙂
Tenhle miniseriál se snažím odkazovat všem, co mají KSP a lítají jen nahoru na silně protáhlou eliptickou dráhu 🙂 Rozhodně je přehlednější, než když se tuto problematiku snažím vysvětlit sám.
Takže za mě: skvělé, přehledné, pochopitelné. Díky 🙂
Velmi mne těší, že naše články jsou čtenářům užitečné 🙂
Dobrý den!
Díky za další zajímavý článek. Chtěl bych se zeptat na jednu situaci, kterou je často vidět ve filmech (napadá mne Apollo 13 a mnohé další) – astronaut usedá za ruční řízení modulu, ze Země dostává pokyn, aby provedl zážeh x vteřin TEĎ. Neohrožený kolega pak svírá v ruce stopky a odpočítává a následuje scéna s úspěšným přistáním/spojením/… Je jasné, že načasování i délka takovéhoto zážehu bude na hony vzdálená ideálnímu výpočtu.
Chtěl bych se proto zeptat, s jakou přesností se vůbec zážehy dělají například právě při změnách drah bez dalších korekcí, které umístí satelity s přesností věřím že v řádu jednotek metrů, v případě spojování lodí pak pak jednotek milimetrů – to už je ale podle mne možná o desítkách korekčních (mikro)zážehů a nikoliv jednom předem spočítaném.
Hezký den,
to, co jsme si popsali v článku bychom moli nazvat „hrubým přechodem“ na oběžnou dráhu. Jak jsem již naznačil v článku – čísla jsou nepřesná kvůli potřebné délce zážehu. Jakmile se sonda dostane na cílovou dráhu, ještě ji drobně poupraví pomocí svými tryskami – provede „jemné korekce“. Ty ostatně provádí po celou dobu své aktivní služby, neboť nikdy není dosažená dráha 100% přesná a jednou za čas je potřeba se opět správně srovnat.
Při dokování dvou těles na oběžné dráze všechno funguje trošičku jinak. V tu chvíli je totiž jedno, jakou rychlostí se tělesa pohybují vůči Zemi. Alfou a omegou je, jakou rychlost mají vůči sobě navzájem a hlavně jakou mají polohu. O měření vzájemných rychlostí se starají radary, s orientací pomáhají laserové zaměřovače na obou tělesech + kamery. Loď, která se připojuje se pak zážehy korekčních trysek ve všech třech osách přibližuje k cílovému bodu.
Pěkně. Díky!
Rádo se stalo
Díky za hezký článek. Něco mi ale není jasné. Z článku vyplývá, že čím je kosmické těleso od centrálního tělesa dál, tím musí mít větší rychlost. Dává mi to i smysl (potřebuji získat větší odstředivou sílu).
Je ale na wikipedii https://cs.wikipedia.org/wiki/Kruhová_rychlost chyba, když v tabulce je úměra nepřímá?
Stejně tak: těleso obíhající při povrchu Země by mělo kruhovou rychlost 7,9 km/s (první kosmická), Měsíc ale obíhá rychlostí „jen“ asi 1 km/s – je dál, ale má menší rychlost.
Míchám tedy různé věci dohromady, nebo je někde chyba? Děkuji za vysvětlení
V první řadě díky za pochvalu. A k dotazu – ano, trochu mícháte jablka a hrušky. Zkusím to vysvětlit. Jsme na nízké oběžné dráze, která je téměř kruhová, to znamená, že je na všech místech zhruba stejně vysoko nad Zemí a tělesno na této dráze má všude téměř stejnou rychlost. Pokud ale budeme chtít dosáhnout oběžné dráhy vyšší, provedeme zážeh, kterým zvýšíme rychlost a naše oběžná dráha se protáhne do elipsy. V jejím nejnižším bude bude mít těleso nejvyšší rychlost a v bodě nejvyšším bude jeho rychlost nejmenší. Laicky a jednoduše řečeno – těleso na protáhlé oběžné dráze mění rychlost za výšku. Když stoupá nahoru, klesá jeho rychlost. Když v nejvyšším bodě oběžné dráhy zapálíme motor, abychom zrychlili, zakulatíme oběžnou dráhu. Rychlost na této dráze bude vyšší, než co mělo těleso v nejvyšším bodě eliptické dráhy, ale přitom bude nižší, než to, co měla na kruhové dráze na nízké oběžné dráze. Pokud byste měl nějaké dotazy, klidně se ozvěte, rád odpovím.
Díky za velmi rychlou odpověď. Musel jsem si ale ještě pár dní nechat, abych to pochopil.
Bylo mi jasné, že čím jsem od Země dál, tím mám menší kruhovou rychlost, abych zůstal na oběžné dráze. Očekával jsem tedy, že tam bude po celou dobu platit tahle nepřímá úměra. Ale pořád mi nebylo jasné, proč to někdy neplatí. Např. „ISS je postupem času zpomalována řídkou atmosférou, takže postupně klesá“. Nebylo mi tedy jasné, proč klesá, když její rychlost se snižuje, ačkoliv v nižší výšce by měla mít rychlost vyšší.
Stejně tak že na vyšší dráze mi stačí nižší rychlost, ale abych se na ni dostal, tak potřebuji zrychlit?
Pak mi ale došlo, že abych změnil výšku oběžné dráhy, tak toho nemůžu docílit tak, že změním rychlost tělesa na tu, kterou by na zamýšlené dráze mělo mít. Protože když těleso zpomalím, tak se odstředivá síla zmenší a těleso začne „padat“ k Zemi.
Stejně tak když těleso zrychlím, tak se odstředivá síla zvětší a těleso se začne od Země vzdalovat.
Ale tím vzdalováním ztrácí pohybovou energii na úkor polohové (předpokládám, že toto pravidlo platí), takže zpomaluje, tím se opět zmenšuje odstředivá síla, těleso je přitahováno více k Zemi a tím opět nabírá rychlost, což se na eliptické dráze pořád opakuje. A úkolem druhého zážehu je zkrátka jen to, abych rychlost tělesa v nejvyšším bodě eliptické dráhy zvýšil na tu, kterou potřebuje na to, aby zůstalo na té vyšší oběžné dráze a tedy „nepadalo“ zpět k Zemi.
Najednou se mi to zdá velmi jednoduché. Předtím mi asi nedošlo hlavně to, že v nejvyšším bodě eliptické dráhy má těleso menší rychlost, než mělo v nejnižším bodě a dokonce nižší, než by mělo mít na vyšší oběžné dráze. Takže mi nevycházelo, že dvakrát zvýším rychlost, ale přesto má být ve výsledku nižší.
Nejlépe jsem to pochopil tak, že jsem si nakreslil obrázek s nižší, vyšší a eliptickou dráhou a doplnil jsem si k tomu ty rychlosti z Vašeho článku. Takže ještě jednou: díky moc a konečně po spoustě let rozumím něčemu, co mi nedávalo smysl (a z diskuzí na internetu nejsem zdaleka jediný).
To mne opravdu těší. 🙂
„Jenže pokud motor hoří mimo apsidu, není už zážeh tolik účinný.“
Je na to důkaz? Oberthův efekt to také nezpochybňuje?
Stačí příklady z praxe – družice, které přechází z GTO na GEO provádí také manévry jen v apoapsidě, když vtahují periapsidu. Naopak když od Země odlétávala sonda Mangalyaan, byla na protáhlé dráze a apoapsidu zvyšovala několika zážehy v periapsidě.