Přiznejme si to upřímně – kosmonautika se hemží spoustou pojmů a zkratek, které jsou pro veřejnost značně nesrozumitelné a těžko pochopitelné. Nemůžeme se tedy divit, že začínající zájemci o kosmonautiku mají z těchto termínů hlavu jako pátrací balón. V dnešním článku se proto pokusím vysvětlit alespoň jednu část kosmonautiky. Věnovat se budeme základním prvkům kosmonautiky, tedy oběžným drahám. Řekneme si jak se dělí, jak se od sebe liší a přidáme i pár zajímavostí.
Pro začátek začneme tím, co je to vůbec oběžná dráha. Není na tom nic těžkého – je to dráha, po které se pohybuje těleso (buďto přirozené – měsíc, hvězda, planeta nebo umělé – družice, sonda, kosmická loď) vesmírem. K tomu, aby se těleso vůbec na oběžnou dráhu dostalo, musí dosáhnout tzv. první kosmické rychlosti. Tato rychlost je na každém tělese jiná a je závislá především na jeho gravitaci. Pro Zemi je to 7,9 km/s a pro Měsíc naopak jen 1,68 km/s. Pokud těleso této rychlosti nedosáhne, nebude kolem planety obíhat, ale bude pouze na tzv. suborbitální dráze – to znamená, že po několikaminutovém pobytu ve vesmíru zamíří zpět do atmosféry.
A nyní přichází první dělení oběžných drah. Pro začátek si dráhy rozdělíme podle toho, kolem kterého tělesa objekt krouží.
Dráha galaktocentrická – tento termín se používá jen málo, ale označují se jím dráhy, po kterých se pohybují např. hvězdy (viz. naše Slunce) okolo jádra galaxie.
Dráha heliocentrická – centrem této soustavy je Slunce. Po této dráze se pohybují například planety, nebo některé družice. Nejsou na ní ale jednotlivé měsíce – ty obíhají okolo svých planet.
Dráha geocentrická – centrem této soustavy je planeta Země. Na této dráze se pohybují všechny telekomunikační, navigační a další družice, létá zde ISS a míří sem naprostá většina startů raket.
Dráha selenocentrická – centrem této soustavy je Měsíc. Po ní obíhají některé vědecké družice.
Každá planeta Sluneční soustavy má vlastní název pro oběžnou dráhu kolem sebe. Důležité je, že tyto názvy se používají naprosto výjimečně a uvádím je spíše jen pro zajímavost.
Merkur – hermocentrická dráha
Venuše – afrodiocentrická dráha
Mars – areocentrická dráha
Jupiter – joviocentrická dráha
Saturn – kronocentrická dráha
Uran – uranocentrická dráha
Neptun – neptunocentrická dráha
Zdroj: http://upload.wikimedia.org/
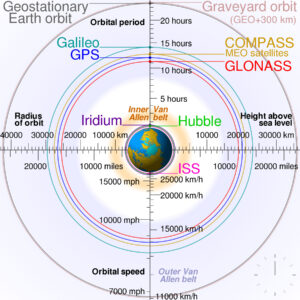
Nyní se přesuneme na dráhu geocentrickou, tedy na dráhu okolo Země. Podíváme se teď na dělení oběžných drah podle výšky ve které se těleso pohybuje.
Nízká oběžná dráha (LEO – low Earth orbit) – Je ze všech drah nejnižší. Začíná nad hranicí atmosféry, tedy zhruba 150 km nad povrchem a končí někde okolo 2 000 km vysoko. Důležité je, že družice na této oběžné dráze jsou chráněné pozemským magnetickým polem. Díky tomu jsou chráněné před kosmickým zářením. Na této dráze se nachází největší množství kosmického odpadu a obíhá tu také ISS.
Střední oběžná dráha (MEO – medium Earth orbit) – začíná ve výšce 2 000 km nad Zemí a končí ve výšce 35 000 kilometrů. Jedná se tedy o poměrně široký pruh, ale nejčastěji se v něm využívá jen malá oblast – okolo výšky 20 000 km nad Zemí. Tady totiž oběžná doba družice činí 12 hodin. Satelit umístěný v této výšce tedy za den oběhne Zemi přesně dvakrát. Ve výšce 20 200 km obíhají družice GPS, ruské Glonassy ve výšce 19 100 km a Galileo je ve výšce 23 222 km. Kromě navigačních družic se sem umísťují třeba satelity, které zajišťují komunikaci v polárních oblastech. Hranice mezi LEO a MEO není ostrá.
Geostacionární dráha (GEO – Geostationary orbit) – tahle dráha je specifickým druhem geosynchronní dráhy (vysvětlíme si později). Její sklon vůči rovníku je 0°. Díky tomu je družice pro pozemského pozorovatele neustále na stejném místě. Toho se využívá třeba u družic pro přenos televizního signálu – pak stačí satelitní parabolu namířit na družici. Tato dráha leží ve výšce zhruba 35 800 km.
Dráha přechodová ke geostacionární (GTO – geostationary transfer orbit) – tato dráha se používá pro vynášení družic na GEO. Především pokud jsou družice moc těžké, nedokázala by je raketa umístit přímo na GEO. Proto je umístí na vysoce eliptickou dráhu, jejíž nejvyšší bod je ve výšce dráhy geostacionární – a právě tahle vysoce eliptická dráha nese zkratku GTO. Družice pak sama svými motory jednak „zakulatí“ oběžnou dráhu na geosynchronní a kromě toho svými zážehy sníží sklon oběžné dráhy na 0°- tím se dostane na geostacionární dráhu – právě na tyto změny je potřeba nejvíc paliva. Proto jsou výhodné starty z kosmodromů blízko rovníku (např. Sea Launch, nebo Kourou). Naopak satelity vynášené z ruských kosmodromů, které leží daleko od rovníku musí provést celou řadu zážehů, než se z GTO dostanou na GEO.
Vysoká oběžná dráha (HEO – high Earth orbit) – oběžná dráha, která začíná za geostacionární dráhou. Není příliš využívaná pro družice, ale velmi často slouží jako odkladiště, nebo chcete-li hřbitov již nepotřebných družic z dráhy geostacionární.

Zdroj: http://upload.wikimedia.org
Zdroj: http://upload.wikimedia.org
Geosynchronní dráha (GSO – Geosynchronnous orbit) – to je dráha, jejíž doba oběhu je stejná, jako doba otočení Země kolem své osy. Díky tomu se z pohledu pozorovatele objekt na této dráze vrací na jedno místo na obloze vždy ve stejný čas každý den. Tato dráha má několik specifických podskupin. Jednou z nich je výše popsaná dráha geostacionární, která má sklon k rovníku 0°.
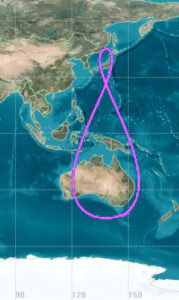
Dráha Tundra – nepříliš často používaný podtyp geosynchronní dráhy – Družice se pohybuje po eliptické dráze se sklonem většinou 63,4°. Díky tomu družice opisuje nad Zemí tvar podobný číslici 8. Díky době oběhu shodné s dobou otočení Země kolem své osy se každý den ve stejnou chvíli objevuje nad stejným místem. To je vhodné třeba pro snímkování, protože pak mají fotky pořízené z různých dnů stejným směrem orientované stíny.
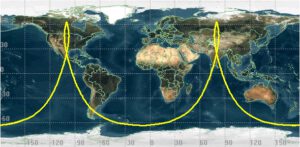
Dráha Molnija – Tato dráha je velmi podobná dráze Tundra. I ona je eliptická a její sklon vůči rovníku činí 63,4°. Co ji ale od Tundry odlišuje je oběžná doba – ta je totiž přesně poloviční. Družice tedy nad místem na Zemi proletí 2x denně. Název pochází od sovětských telekomunikačních družic Molnija,které využívaly právě této dráhy. Ostatně přiložený obrázek velmi dobře ilustruje povahu dráhy Molnija.
Zdroj: http://upload.wikimedia.org
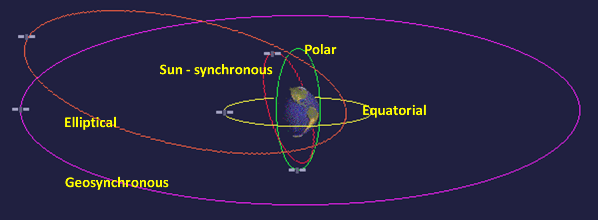
Další kategorie podle které můžeme oběžné dráhy dělit je podle jejich orientace, tedy podle jejich sklonu vůči rovníku.
Dráha prográdní – Družice při ní letí od západu na východ, díky čemuž využívá zemské rotace. Sklon dráhy je v tomto případě 0° – 90°.
Dráha polární – Tato dráha má sklon oproti rovníku 90°. Díky tomu přelétá satelit přes oba zemské póly.
Dráha retrográdní – Družice vyslaná na tuto oběžnou dráhu letí proti směru otáčení Země. Sklon její dráhy je v rozmezí 90° – 180°.
Existuje samozřejmě ještě mnoho dalších dělení, například na dráhy kruhové a eliptické. Za zmínku stojí i dráha heliosynchronní – družice na ní umístěná vychází a zapadá nad obzorem vždy ve stejný čas každý den. Díky tomu je povrch vždy osvětlen takřka ze stejného úhlu. Toho využívají třeba mapovací, ale i vojenské satelity, nebo meteorologické družice. Typická heliosynchronní dráha se nachází ve výšce 600 – 800 km nad Zemí, má sklon 98° (je tedy téměř polární a lehce retrográdní) a oběžná doba činí 96 minut – tím pádem oběhnou kolo Země každý den 15x. Kromě toho známe i dráhy otevřené, tedy únikové, kdy těleso dosáhne určité (únikové) rychlosti a opustí gravitační sféru svého původního tělesa, ale výše nastíněné dělení v základu stačí.
Na závěr bych chtěl poznamenat, že tento článek byl určen především pro začátečníky, kteří se v kosmonautice teprve rozkoukávají. Právě z toho důvodu jsem se nevěnoval elementům dráhy. Pokud bych tady měl rozebírat velkou poloosu, délku vzestupného uzlu, nebo argument šířky pericentra (elementů dráhy je celkem 6 + čas), zalepil bych čtenářům hlavy jen jejich vysvětlením. Doufám tedy, že v kosmonautice zběhlejší čtenáři při čtení předchozích řádků příliš neprskali a naopak že začátečníkům takovéto rozdělení pomohlo k pochopení alespoň základních druhů oběžných drah.
Zdroje informací:
http://en.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
http://en.wikipedia.org/
Zdroje obrázků:
http://www.3dnews.ru/_imgdata/img/2012/05/04/628763/19528a4.jpg
http://upload.wikimedia.org/wikipedia/commons/thumb/b/b4/Comparison_satellite_navigation_orbits.svg/1000px-Comparison_satellite_navigation_orbits.svg.png
http://upload.wikimedia.org/wikipedia/commons/8/82/Orbitalaltitudes.jpg
http://upload.wikimedia.org/wikipedia/commons/c/c2/Qzss-45-0.09.jpg
http://upload.wikimedia.org/wikipedia/commons/b/bf/Molniya.jpg





Díky, myslím že takováto osvěta je výborná. Budou další díly na jiná témata? Taková kosmonautika pro začátečníky 🙂
BTW dotaz – když se vynáší družice na polární dráhu, tak startují rakety 90° k rovníku? Nebo startují vždy „s rotací“ Země až na orbitě „zahnou“?
Ohledně dalších dílů – Nevím, uvidíme. Muselo by mě nějaké téma napadnout. 🙂
A k dotazu – při startu na polární dráhy míří raketa od začátku vytyčeným směrem. Pokud by nejprve letěla na západ a pak se stáčela na sever, pak by jen zbytečně plýtvala palivem.
Právě z těchto důvodů se využívají různé kosmodromy – některé mají „střelecký prostor“ na východ, jiné na sever – z těch se startuje na polární dráhy.
Nechci rejpat, ale napadají mě témata, která by v tomto duchu zasloužilo zpracovat. Možná by stálo za to probrat i meziplanetární dráhy, jak klasické Hohmanovy, tak gravitační manévry, kombinované manévry (jako casini) a zhruba jejich tvorba, aerobraking. Potom mě napadají třeba paliva kosmických raket, výhody, nevýhody, trendy a plány. Komunikace se sondami a stanicemi dnes a v minulosti.
Ty meziplanetární dráhy by nemusely být špatné. Zároveň by se s tím mohly spojit i základy pohybu na oběžné dráze – apsidy a zážehy v nich. A i paliva nevypadají špatně. Možná něco sepíšu. 😉
Když už jsme u těch otázek; kruhová dráha je asi jasná, ale jak to je s těmi eliptickými?
Eliptické dráhy mají dva hlavní body – Periapsidu (v případě, že jsou kolem Země, pak mluvíme o Perigeu) – v ní je družice (nebo jiný objekt) cílovému tělesu nejblíže a má v něm také největší rychlost. Druhým důležitým bodem, který leží „na druhé straně elipsy“ je Apoapsida (v případě Země Apogeum). V tomhle bodě je družice naopak nejdále od středového tělesa a má v tomhle bodě nejmenší rychlost.
Snad jsem to popsal srozumitelně 🙂
pri tomto by ma zaujímalo, ako je to so zmenou dráhy npr. z kruhovej na eliptickú (prip. naopak). Mení sa pri tomto jednoducho len rýchlosť, alebo sú v tom zahrnuté aj nejaké iné manévre?
Pokud se bavíme čistě jen o „zakulacení dráhy“ z elipsovité na téměř kruhovou, nebo naopak „protažení“ dráhy do elipsy, pak se opravdu mění jen rychlost. Pokud přijde zážeh ve směru letu, pak protilehlá apsida stoupá, pokud loď zažehne motory proti směru letu, pak protilehlá apsida klesá.
Hmmm takhle stručně popsané je to asi nesrozumitelné. Asi udělám další díl, kde se budu těmhle základním manévrům věnovat trochu podrobněji. 🙂
Dik, za odpoveď Dušan, myslím, že tak zhruba tomu rozumiem aj v tom stručnom podaní.
Mimochodem, Petře, pokud se nestane nic mimořádného, tak v pondělí vyjde můj další článek, který se bude věnovat právě základním manévrům na oběžné dráze, ve kterých nebude chybět ani zakulacování dráhy a další manévry. 😉
Perfektní článek! Doufám, že přijde i Průvodce po oběžných drahách level 2 a jiní Průvodci 😉 jak navrhoval indian22. Mě ještě napadlo rozdělení raket, počty stupňů, vysvětlení „polovičního“ stupně, crosfeed, a stím vším související složitost, resp. jednoduchost konstrukce, palivová náročnost, nosnost atd.
Díky 🙂
Zhruba za půl hodinky vyjde volné pokračování 😉
Navrhuji ke každému pojmu dokreslit jednoduchý ilustrativní obrázek.
Ne každý má tu prostorovou představivost
Ilustračních obrázků je v článku, podle mého názoru, docela dost. Díky tomu by měl článek pochopit i člověk se slabší prostorovou představivostí.
Umí mi někdo polopatě vysvětlit, proč např. geostacionární družice nemohou létat i ve výšce např. 20 000 km? Proč to není možné – když se přizpůsobí rychlost družice – tedy v tomto případě, když se rychlost sníží? Copak má snížení výšky a rychlosti nutně za následek nemožnost dosažení kruhové dráhy? Pokud jo, tak proč ??? (jasněže ta rychost musí být aspoň 1. kosmická…)
Hezký den,
zkusím to vysvětlit. Začnu obecně, ale dostanu se k tomu. Na oběžné dráze jsou rychlost a výška dvěma stranami jedné mince – jedna veličina ovlivňuje druhou. Tělesa na nízkých oběžných drahách obíhají mateřské těleso rychleji, než tělesa na vzdálenějších drahách. Jednoduchý příklad – ISS ve výšce cca. 400 km obkrouží kolem Země jednou za 90 minut. Naopak Měsíc, vzdálený nějakých 300 000 km, oběhne kolem Země za nějakých 28 dní. Téměř kruhová oběžná dráha se dá dosáhnout kdekoliv – ať už na nízké, nebo vysoké oběžné dráze, v tom pes zakopaný není.
Hlavní je, že tělesa na geostacionární dráze mají oběžnou dobu kolem Země shodnou s dobou otočení Země kolem své osy – tedy přibližně 24 hodin. Této rychlosti dosáhnou tělesa pouze na dráze ve výšce cca. 35 800 km. Pozorovateli ze Země se pak zdá, že družice visí nehybně na jednom místě oblohy.
Pokud bychom nějakou družici umístili na oběžnou dráhu ve výšce Vámi zmiňovaných 20 000 km (takové družice existují – do této výšky se dávají navigační satelity GPS, Glonass, Galileo), tak by jejich oběžná doba kolem Země činila cca. 12 hodin. Sám vidíte, jak výška oběžné dráhy ovlivňuje rychlost oběhu. Aby družice visela stále nad jedním bodem, musí být její oběžná doba 24 hodin a nějaké drobné. Toho se dá dosáhnout pouze ve výšce 35 800 km.
Pokud jsem o vysvětlil málo „polopaticky“, klidně se ozvěte a já rád upřesním případná bílá místa.
Bohužel tomu stále nerozumím. Zkusím naznačit způsob mé dedukce (všechny poznatky mám jen z „pozemské“ fyziky), pro jednoduchost budu předpokládat pouze kruhové dráhy:
Ve výšce 20 000 km je délka dráhy 2*Pí*R=2*3,14*(6380+20000)=165 666km.
Pro oběžnou dobu 12 hodin je obvodová rychlost v=dráha/čas=165666/(12*3600)=3,83 km/s.
Pokud je tato úvaha správná, tak můj dotaz je tento: Proč v těch 20000 km nad zemí nemůžeme té družici udělit nižší (nebo i vyšší) rychlost, aby Zemi oběhla např. za 15 hodin? Ta rychlost by pak musela být v=165666/(15*3600)=3,07 km/h. (Nebo pro oběžnou dobu 9 hodin by byla rychlost 5,11 km/s.)
To by ta dráha už nebyla kruhová, nebo by družice spadla?
Zkusím to vysvětlit. Pokud jsme na oběžné dráze ve tvaru kruhu a zpomalili bychom, pak už oběžná dráha nebude kruhová, ale eliptická. Takhle jak to popisuju to zní možná divně a složitě, ale zkuste si zahrát hru Kerbal Space Program. V ní všechno velmi snadno pochopíte.
Pro Karla:
Zkusme použít jednoduchou analogii: mějme vhodné těleso, přivažme ho na provázek, druhý konec provázku držme v ruce a začněme točit. Naše ruka představuje Zemi a těleso družici. Zjistíme, že abychom dosáhli kruhové dráhy, musíme točit dostatečně rychle.
Pokud točíme pomaleji a rovina obíhání je rovnoběžná se zemí, opisuje provázek s tělesem kužel.
Je-li rovina obíhání kolmá k zemi a točíme pomaleji, těleso při cestě k horní úvrati padá – kruhové dráhy dosáhneme až tehdy když ho roztočíme dostatečně rychle. A máme analogii s první kosmickou rychlostí.
Čím vice provázek prodlužujeme, tím pomaleji můžeme točit. Analogicky družice obíhající kolem Země musí obíhat tím rychleji, na čím nižší dráze je. Je to způsobeno gravitační silou, která sice působí donekonečna, její intenzita ale klesá se čtvercem vzdálenosti. Zpomalíme-li tedy družici z vašeho příkladu pod kritickou rychlost, tato družice spadne na Zemi. Zrychlíme-li nad kritickou mez, dosáhneme druhé kosmické rychlosti a družice odletí od Země pryč.
Pak ještě existuje třetí kosmická rychlost, která těleso může odeslat ze Sluneční soustavy do mezihvězdného prostoru.
Chceme-li v naší analogii pokračovat a demonstrovat eliptické dráhy, použijeme místo provázku gumičku – a teď nastává ta správná legrace, pružnost gumičky nám umožní vykreslit různé oběžné dráhy, byť tady naše analogie už trochu pokulhává 🙂
Neví někdo o kolik kilometrů je vychílená oběžná dráha země?
Trochu nechápu otázku. Sklon rotační osy vůči kolmici k ekliptice se neměří v kilometrech, ale ve stupních. Je to přesně 23,439 281°.
Pokud máte na mysli excentricitu (výstřednost) oběžné dráhy Země kolem Slunce, tak v nejbližším místě (perihel) je Země ke Slunci 147 098 074 km, kdežto v nejvzdálenějším (afel) je to 152 097 701 km. Rozdíl je tedy necelých 5 milionů kilometrů.
Dobrý deň, včera sme debatovali pri pive na témy okolo obežných dráh a rýchlostí. Väčšinu odpovedí som našiel na týchto stránkach, kde je to pekne zrozumiteľným štýlom vysvetlené, za čo Vám ďakujem. Jednu otázku by som predsa len mal. Bavili sme sa aj o balistických raketách (USA vs. Rusko) a nevedeli sme sa zhodnúť v tom, či z titulu smeru rotácie Zeme je rozdiel v čase letu, prípadne množstve paliva, ak letí raketa z Ruska na USA alebo z USA na Rusko. Pri predpoklade, že letia po jednej trajektórii, len v opačných smeroch. Ak je vôbec možné dosiahnuť uvažovanú rovnakú trajektóriu. Ďakujem za odpoveď.
Vlado Medvec
Hezký den,
těší nás, že Vám článek pomohl. Co se týče Vaší otázky, tak je pravda, že pokud raketa letí proti směru otáčení Země, tedy z východu na Západ, má trochu těžší situaci protože jí nepomáhá zemská rotace. U balistických střel ale tento problém není tak markantní jako u raket orbitálních, nicméně určité procento rozdílu tam je.
Pro lepší pochopení základů orbitální mechaniky a orbitálních manévrů, doporučuji PC Hry jako je „Orbiter“ nebo „Kerbal Spaceprogram“.
Orbiter je Hardcore simulace, takže doporučuji pouze lidem kteří jsou kosmonautikou vyloženě posedlí.
Kerbal spaceprogram je mírnější, vhodný pro běžného člověka, ovšem podán v poněkud „dětské formě“.
KSP je určitě super, sám jej v některých článcích doporučuji.
nenasel jsem cislunarni drahu.
To je tím, že nic jako cislunární dráha neexistuje. Existuje pouze tzv. cislunární prostor, což je oblast, která je velmi volně ohraničena geostacionární oběžnou drahou na straně jedné a oběžnou dráhou Měsíce na straně druhé. V tomto prostoru je možné využívat celou řadu oběžných drah – od těch jednoduchých až po komplexní, protože se zde již projevuje gravitace Měsíce. Některé prameny do cislunárního prostoru řadí např. i některé hodně protáhlé retrográdní oběžné dráhy kolem Měsíce.
jo pravda. spletl jsem prostor s drahou. ma tam obihat nova stanice kolem mesice. zajimalo by me jak muze draha vypadat. jestli ma byt stanice porad v dosahu komunikace se zemi a zaroven porad osvetlena sluncem.
Očekává se, že stanice bude své dráhy měnit. Jak už jsem psal, v tomto prostoru je mnoho možností a přecházení mezi nimi potřebuje jen relativně malou změnu rychlosti a tedy málo paliva.
Pátral jsem kde se jako začátečník dočtu jak je to s oběžnýma dráhama a super článek.
Díky moc, jsem rád, že se článek hodí!
Když je dráha eliptická, centrální těleso je v ohnisku elipsy, tak nějak chápu jaký síly tam jsou, jak to funguje, asi to jinak být nemůže, ale neumím si představit proč by centrální těleso nemohlo být ve středu elipsy. I kdyby ta dráha byla nějak nestabilní, není možný, aby elipsa byla takhle vycentrovaná?
Dobrý den,děkuji za článek,hezky vysvětleno.
Měla bych jednu otázku.
Putuje ISS po stejné dráze a jestli ano,proč je vidět po několika dnech z pohledu pozorovatele na jiném místě a jestli za to může rotace země nebo sklon k rovníku.
Děkuji za odpověď
H.Pluskalová
Hezký den,
přesně tak. ISS je stále na stejné dráze (samozřejmě drobně manévruje, ale to pro naše účely není podstatné). Důležité je, že se pod ní naše Země otáčí – oběh ISS trvá 92 minut, den má 24 hodin, což nejde 92 minutami vydělit beze zbytku – díky tomu stanice přelétává každý den nad trochu jiným místem a postupně takhle přeletí nad celou Zemí od 51. jižní po 51. severní rovnoběžku.
Dobrý den,potřebuji poradit.JWST má být umístěn v lagrangeově bodě asi 1.5 mil.km. od země.Je pravda,že to je místo s nejmenším působením gravitačních sil,protože mě to přijde ještě pořád dost blízko na absenci takových sil.Děkuji za odpověď.Hela
Hezký den,
ano, JWST bude v libračním centru L2 soustavy Slunce-Země. Tento librační bod patří mezi pět libračních center soustavy dvou těles(zde Slunce a Země), ve kterých je gravitační působení stejné. Není to tak, že by tam ty síly nebyly, pouze se vyrovnávají. Wikipedie říká, cituji:
Librační centrum (librační bod, Lagrangeův bod) je v nebeské mechanice takový bod v soustavě dvou těles m1 a m2 rotujících kolem společného těžiště, v němž se vyrovnávají gravitační a odstředivé síly soustavy tak, že malé těleso umístěné do tohoto bodu nemění vůči soustavě svou polohu (zachovává od m1 i m2 konstantní vzdálenost).